GNNs: Melhorando Modelos de Machine Learning com Grafos

No campo do Machine Learning, é comum trabalhar com dataframes compostos por inúmeras linhas de features, que são utilizadas para treinar modelos visando prever rótulos com a máxima acurácia possível. Um desafio adicional é a construção de features a partir de dados brutos para aprimorar o desempenho do modelo. Frequentemente, esse processo ignora as relações existentes entre os dados, resultando na perda significativa de informações valiosas. Considerar essas interconexões pode revelar informações importantes e que aprimoram significativamente a performance dos modelos.
Em dados de redes sociais, por exemplo, é simples construir features de um usuário relacionadas à quantidade de postagens, conteúdo ou frequência. No entanto, não é tão simples criar features sobre como os posts de um usuário estão conectados entre si e com outros usuários, nem sobre os usuários interagem entre si ao longo do tempo. Em análise de risco de crédito, é relativamente simples criar features sobre o total de gastos ou o nível de endividamento de um usuário. Contudo, capturar features sobre a ordem em que os gastos ocorrem ou quais gastos estão conectados de alguma forma é mais desafiador.
Em resumo, capturar as interconexões existentes em um conjunto de dados é muito mais difícil do que tratar os dados como independentes entre si.
Um Exemplo Prático: O Dataset Cora
Vamos considerar um exemplo prático com o dataset Cora, que contém 2708 publicações segmentadas em 7 categorias diferentes. Cada publicação é expressa como um conjunto de 1433 features binárias, representando a existência de palavras em uma publicação, ou seja, um modelo bag of words. O objetivo é predizer a qual das 7 categorias cada publicação pertence.
O caminho clássico
Podemos abordar esse problema de forma clássica, treinando um modelo Random Forest para prever as classes e obtendo uma acurácia de 0.56. Embora possamos otimizar esse modelo de diversas maneiras para melhorar esse resultado, esse não é nosso objetivo aqui.
from torch_geometric.datasets import Planetoid
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
import pandas as pd
import Planetoid
dataset = Planetoid(root='.', name='Cora')
data = dataset[0]
df_x = pd.DataFrame(data.x.numpy())
df_x['label'] = pd.DataFrame(data.y)
X = df_x.iloc[:, :-1]
y = df_x.iloc[:, -1]
train_mask = data.train_mask.numpy()
test_mask = data.test_mask.numpy()
X_train = X[train_mask]
y_train = y[train_mask]
X_test = X[test_mask]
y_test = y[test_mask]
model = RandomForestClassifier(random_state=42)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f'Acurácia do modelo: {acc:.2f}')Acurácia do modelo: 0.56
Explorando o Grafo
Esse dataset tem uma característica interessante: temos informações sobre quais publicações foram citadas por outras. Ou seja, cada linha do dataset está interconectada com outras linhas. Na abordagem tradicional com Random Forest, essa informação foi ignorada. Explorando essa característica, podemos tratar o dataset como um grafo, onde cada publicação é um vértice e a existência de uma citação define uma aresta entre dois vértices.

Vamos relembrar o comportamento de uma rede neural tradicional. Nesse caso, cada camada da rede representa uma transformação linear aplicada aos dados de entrada. Se cada linha "a" do dataset (ou cada vértice, se entendermos como um grafo) for representada por "x_a", então a transformação linear será uma multiplicação dessa entrada por uma matriz de pesos W.
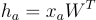
Treinando um modelo MLP simples com duas camadas lineares, obtemos um resultado parecido com o do Random Forest, com acurácia de 0.56.
import torch
torch.manual_seed(0)
from torch.nn import Linear
import torch.nn.functional as F
def accuracy(y_pred, y_true):
"""Calculate accuracy."""
return torch.sum(y_pred == y_true) / len(y_true)
class MLP(torch.nn.Module):
def __init__(self, dim_in, dim_h, dim_out):
super().__init__()
self.linear1 = Linear(dim_in, dim_h)
self.linear2 = Linear(dim_h, dim_out)
def forward(self, x):
x = self.linear1(x)
x = torch.relu(x)
x = self.linear2(x)
return F.log_softmax(x, dim=1)
def fit(self, data, epochs):
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(
self.parameters(), lr=0.01, weight_decay=5e-4
)
self.train()
for epoch in range(epochs + 1):
optimizer.zero_grad()
out = self(data.x)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
acc = accuracy(
out[data.train_mask].argmax(dim=1), data.y[data.train_mask]
)
loss.backward()
optimizer.step()
@torch.no_grad()
def test(self, data):
self.eval()
out = self(data.x)
acc = accuracy(
out.argmax(dim=1)[data.test_mask], data.y[data.test_mask]
)
return acc
mlp = MLP(dataset.num_features, 16, dataset.num_classes)
print(mlp)
mlp.fit(data, epochs=200)
acc = mlp.test(data)
print(f'Acurácia do modelo: {acc:.2f}')Acurácia do modelo: 0.56
Capturando Relações em Grafos
Nos grafos, queremos capturar as relações entre um vértice e todos os seus vizinhos. A existência dessa conexão define a existência de uma aresta entre os vértices, tornando-os vizinhos. Podemos definir a vizinhança de um vértice "a" como "N_a". Ou seja, "N_a" é o conjunto de todos os vértices vizinhos do vértice "a". Uma forma de agregar as informações dos vizinhos de um vértice é usando alguma agregação, como uma soma. A equação que define a saída "h_a" de uma camada linear em uma rede neural pode ser reescrita para representar essa operação nos grafos.
Assim como antes, temos uma transformação linear proporcionada pela multiplicação de uma matriz W pela entrada X. Diferente da anterior, aqui temos um somatório que agrega o resultado para todos os vizinhos do vértice a, incluindo a relação de adjacência entre esses vértices no modelo.
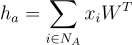
A forma matricial de realizar essa operação sem a necessidade de um somatório explícito é incluindo a matriz de adjacências na operação. Dessa forma, a multiplicação das matrizes soma os valores de acordo com a existência de uma aresta entre eles. Na fórmula abaixo, Ã é a soma da matriz de adjacências A com uma matriz identidade I, Ã = A + I. Isso porque, na matriz de adjacências original, um nó nunca está conectado a ele mesmo, então sua informação seria ignorada na transformação linear. Queremos incluir não somente a informação dos vizinhos, mas também a do próprio nó, daí a necessidade dessa soma.
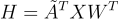
Vanilla GNNs
Uma "Vanilla GNN Layer" normalmente se refere a uma camada simples de convolução em grafos. Pode ser implementada de várias maneiras, mas a ideia central é que ela processa as características dos nós e as atualiza com base na estrutura do grafo e nas características dos nós vizinhos.
Podemos definir uma camada simples de GNN para realizar essa operação, como no código a seguir. Note que essa camada possui uma transformação linear, seguida por outra baseada na matriz de adjacências, somando as características do nó e seus vizinhos logo após a transformação linear para que a rede aprenda essas interconexões.
import torch
from torch.nn import Linear
from torch_geometric.utils import to_dense_adj
import torch.nn.functional as F
class VanillaGNNLayer(torch.nn.Module):
def __init__(self, dim_in, dim_out):
super().__init__()
self.linear = Linear(dim_in, dim_out, bias=False)
def forward(self, x, adjacency):
x = self.linear(x)
x = torch.sparse.mm(adjacency, x)
return x
adjacency = to_dense_adj(data.edge_index)[0]
adjacency += torch.eye(len(adjacency))
Por fim, podemos repetir nosso modelo MLP com a mesma estrutura, mas trocando a camada linear simples por uma camada GNN. Dessa forma, o modelo aprenderá as relações entre os dados.
class VanillaGNN(torch.nn.Module):
def __init__(self, dim_in, dim_h, dim_out):
super().__init__()
self.gnn1 = VanillaGNNLayer(dim_in, dim_h)
self.gnn2 = VanillaGNNLayer(dim_h, dim_out)
def forward(self, x, adjacency):
h = self.gnn1(x, adjacency)
h = torch.relu(h)
h = self.gnn2(h, adjacency)
return F.log_softmax(h, dim=1)
def fit(self, data, epochs):
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(self.parameters(),
lr=0.01,
weight_decay=5e-4)
self.train()
for epoch in range(epochs+1):
optimizer.zero_grad()
out = self(data.x, adjacency)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
acc = accuracy(out[data.train_mask].argmax(dim=1),
data.y[data.train_mask])
loss.backward()
optimizer.step()
@torch.no_grad()
def test(self, data):
self.eval()
out = self(data.x, adjacency)
acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])
return acc
gnn = VanillaGNN(dataset.num_features, 16, dataset.num_classes)
print(gnn)
gnn.fit(data, epochs=200)
acc = gnn.test(data)
print(f'\nAcurácia do modelo: {acc:.2f}')Acurácia do Modelo: 0.77
Conclusão
Ao incluir uma simples operação de convolução em grafos, conseguimos aumentar a acurácia do modelo de 0.56 para 0.77. Esse resultado demonstra o potencial de considerar as relações entre os dados, além das características individuais. Embora essa abordagem tenha levado a uma melhoria significativa, vale ressaltar que a estrutura utilizada é bastante simples e há potencial para avanços ainda maiores.
Existem muitas outras arquiteturas mais sofisticadas, como Graph Attention Networks (GATs) e outras variantes de GNNs, que podem capturar ainda mais nuances nas interconexões dos dados. Explorar essas técnicas pode trazer benefícios adicionais, especialmente em datasets mais complexos.
Essa abordagem pode ser aplicada a diversos domínios, como redes sociais, análise de crédito, biologia computacional e muitos outros. A chave é sempre considerar como as relações entre os dados podem ser aproveitadas para extrair mais informações e, assim, construir modelos mais robustos e precisos.



