O problema de detecção de comunidades em grafos
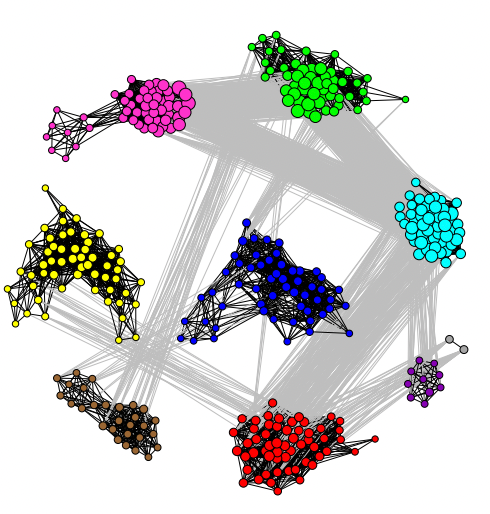
No último post eu falei sobre o que é um grafo e alguma de suas aplicações. Hoje eu quero falar sobre uma aplicação específica que é a minha preferida. Me refiro ao problema de detecção de comunidades.
Lembre-se que um grafo é composto por um conjunto de vértices e um conjunto de arestas que conectam os vértices. Nesse contexto, uma comunidade é um grupo de vértices que compartilham características comuns e os fazem ser "semelhantes"na estrutura do grafo.
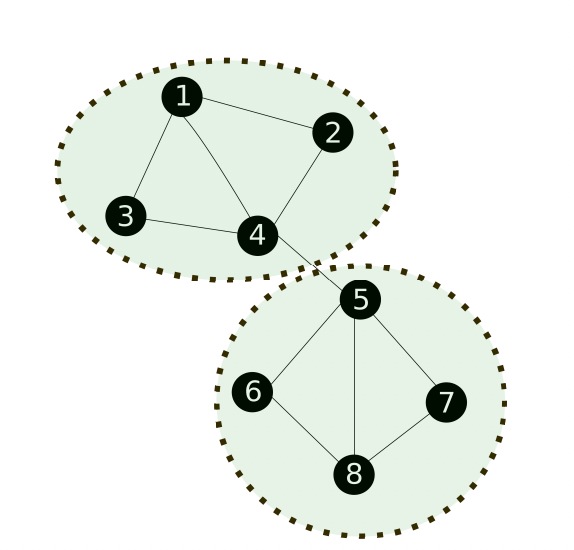
A imagem abaixo representa um grafo com 8 vértices conectados entre si. Esse grafo foi dividido em 2 comunidades, cada uma contendo 4 vértices. Repare que esses vértices estão mais conectados entre si do que com o restante do grafo. O vértice 1, por exemplo, possui conexões com os vértices 2, 3 e 4. Ao mesmo tempo, ele não possui nenhuma conexão com os vértices 5, 6, 7 ou 8.
De modo geral, o problema de detecção de comunidades consiste justamente em encontrar esses grupos de vértices que possuem uma quantidade muito maior de conexões entre si do que com o restante do grafo. Embora no exemplo dado aqui a resposta pareça bem óbvia, o problema se torna extremamente desafiador quando estamos falando de dados do mundo real.
Esse dificuldade surge como consequência do volume de dados, visto que os grafos podem facilmente possuir milhares de vértices e se torna impossível visualizar a estrutura como fizemos aqui.
Mas... pra que serve?
O problema de detecção de comunidades em grafos possui inúmeras aplicações, mas vou abordar apenas uma aqui: sistemas de recomendação.
Imagine um ecommerce com diversos produtos. Você acessou e realizou uma compra de um determinado produto. Obviamente, produtos similares ao que você comprou serão exibidos para você. Mas... como essa escolha é feita? como identificar quais produtos são similares?
Existam inúmeras formas de fazer isso, mas eu quero discutir esse problema usando grafos. Imagine que cada produto é um vértice e esses produtos estão conectados entre si se compartilharem determinadas características. Essas características podem ser, por exemplo, categoria, cor ou tamanho. Quanto mais características em comum, maior a força da conexão entre esses vértices.
Nesse contexto, uma comunidade representaria um grupo de vértices que possuem diversas características em comum. Imagine que um produto seja uma camiseta azul de tamanho M com estampa X. No grafo, esse vértice pertenceria a mesma comunidade de outros produtos similares, como uma camiseta azul de tamanho M com estampa Y. Isso aconteceria porque ambos os produtos são camisetas da cor azul e possuem tamanho M. Ou seja, eles possuem muitas características em comum e sua conexão no grafo é forte.
Se alguém visitou a camiseta azul de tamanho M com estampa X, provavelmente a camiseta azul de tamanho M com estampa Y também irá atrair seu interesse. Vamos repetir essa frase de uma forma mais formal e matemática: se alguém visitou um produto (que representa um vértice no grafo), provavelmente esse visitante também irá se interessar por outros produtos similares (representados por vértices do grafo que estão na mesma comunidade).
Percebe como um problema de recomendação de produtos similares em um ecommerce pode ser interpretado como um problema de detecção de comunidades em grafos?
Esse é apenas um exemplo, mas diversas outras aplicações podem ser abordadas dessa forma, como identificação de fraudes, por exemplo. Mas isso fica pra outro dia.



