Modelando a incerteza: como decidir com poucos dados

Em marketing digital, growth e otimização de produtos, testes A/B são tratados como instrumentos de precisão cirúrgica. Um botão azul contra um verde. Uma cópia com verbo direto contra uma mais emocional. Basta rodar o experimento, olhar o p-valor e decidir.

Mas quando as taxas de conversão são baixas — e quase sempre são —, essa precisão é ilusória. A estatística frequentista tradicional, com seus testes z e p-valores, frequentemente falha em capturar a verdadeira incerteza envolvida. Um p-valor alto pode esconder um sinal real. Um p-valor baixo pode amplificar um efeito frágil. E nesse ruído, boas decisões morrem na dúvida.

A estatística bayesiana oferece uma alternativa mais realista e, muitas vezes, mais útil. Ela não se limita a rejeitar hipóteses nulas: constrói uma distribuição explícita sobre o que acreditamos ser verdade. Em vez de perguntar “isso é estatisticamente significativo?”, passamos a perguntar:

→ “Com que grau de confiança posso afirmar que a nova versão é melhor? E quanto melhor ela é, exatamente?”

Neste artigo, vamos simular um cenário realista de teste A/B com conversões de 0.3% e 0.5%, aplicando tanto abordagens frequentistas quanto bayesianas. Vamos comparar não apenas os resultados, mas principalmente os modelos mentais que cada abordagem impõe. O objetivo aqui não é defender uma escola estatística, mas explorar onde certos métodos tropeçam quando mais precisamos deles — e o que podemos fazer para enxergar com mais clareza.

Modelagem Inicial: Simulando um Cenário Realista

Começamos com o básico: dois grupos, 5.000 visitantes cada.

A versão A (controle) converte 0.3% dos visitantes. Isso significa que, em média, 15 a cada 5.000 visitantes compram, clicam ou realizam a ação desejada. Já a versão B (variante) tem uma taxa um pouco maior: 0.5%. Parece pouco? Em grandes volumes ou produtos de alto valor, esse 0.2 ponto percentual pode representar milhões em receita.

Para simular, usamos uma distribuição binomial: cada visita é um experimento independente com probabilidade de sucesso conhecida.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random

# Simulando 1000 visitantes para cada versão
visitors_A = 5000
visitors_B = 5000

random.seed(56)

def page_conversion(taxa_conversao):
    return int(random.random() < taxa_conversao)

def simulate_experiment(visitors_A, visitors_B, taxa_A, taxa_B):
    conversoes_A_dist = np.array([page_conversion(taxa_A) for _ in range(visitors_A)])
    conversoes_B_dist = np.array([page_conversion(taxa_B) for _ in range(visitors_B)])
    return conversoes_A_dist, conversoes_B_dist

# Taxas reais de conversão
taxa_A = 0.003
taxa_B = 0.005

# Geração binária: 1 = converteu, 0 = não converteu
conversoes_A_dist, conversoes_B_dist = simulate_experiment(visitors_A, visitors_B, taxa_A, taxa_B)

conversoes_A = conversoes_A_dist.sum()
conversoes_B = conversoes_B_dist.sum()

print(f"Conversões A: {conversoes_A} / {visitors_A}")
print(f"Conversões B: {conversoes_B} / {visitors_B}")

Numa execução típica, vemos algo como:

Conversões A: 20 / 5000
Conversões B: 25 / 5000

Diferença de 0.1 ponto percentual. Insignificante? Ruído? Evidência real? Essa é a pergunta que todo profissional de produto precisa responder — e a estatística deve ajudar.

Frequentismo: O Limite do P-Valor

Aplicando o teste z para proporções:

from statsmodels.stats.proportion import proportions_ztest

counts = np.array([conversoes_B, conversoes_A])
nobs = np.array([visitors_B, visitors_A])

stat, pval = proportions_ztest(count=counts, nobs=nobs)
print(f"p-valor: {pval:.4f}")
# p-valor: 0.4550

Um p-valor de 0.4550. Pela convenção, isso nos impediria de rejeitar a hipótese nula. Conclusão? Não houve evidência suficiente para rejeitar a hipótese nula. Mas será que isso significa que não há diferença?

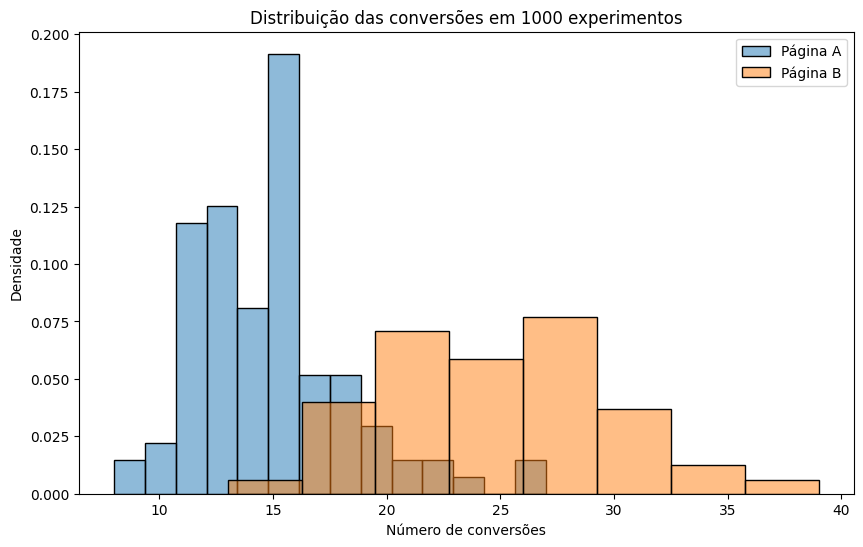
E se repetirmos esse experimento milhares de vezes, mantendo as mesmas taxas verdadeiras (0.3% e 0.5%)? Você verá algo curioso:

• Em vários testes, A “vence” B — mesmo com a taxa real sendo menor.
• Em outros, B vence com folga.
• A variabilidade é enorme.

Isso evidencia o ponto central: com amostras pequenas e eventos raros, o p-valor oscila mais do que gostaríamos. Ele depende da amostra específica e responde a uma pergunta condicional: ‘quão improvável seria observar um resultado tão extremo quanto o que vimos, se a hipótese nula fosse verdadeira?’ — mas não nos diz a probabilidade da hipótese nula ser verdadeira.

from tqdm import tqdm

def run_multiple_experiments(experimentos, visitors_A, visitors_B, taxa_A, taxa_B):
    conversions_A_list = []
    conversions_B_list = []

    for _ in tqdm(range(experimentos)):
        conv_A, conv_B = simulate_experiment(visitors_A, visitors_B, taxa_A, taxa_B)
        conversions_A_list.append(conv_A.sum())
        conversions_B_list.append(conv_B.sum())

    # Convertendo para arrays numpy para facilitar comparações
    conversions_A_arr = np.array(conversions_A_list)
    conversions_B_arr = np.array(conversions_B_list)
    
    plt.figure(figsize=(10,6))
    sns.histplot(conversions_A_arr, label='Página A', alpha=0.5, stat='density')
    sns.histplot(conversions_B_arr, label='Página B', alpha=0.5, stat='density')
    plt.xlabel('Número de conversões')
    plt.ylabel('Densidade')
    plt.title('Distribuição das conversões em 1000 experimentos')
    plt.legend()
    plt.show()
    
    
run_multiple_experiments(100, visitors_A, visitors_B, taxa_A, taxa_B)

Intervalo de Confiança: Uma Lente Parcial

Dentro do paradigma frequentista, uma alternativa ao p-valor é o intervalo de confiança para a diferença entre as taxas de conversão. Em vez de apenas declarar "significativo ou não", ele mostra uma faixa plausível onde a verdadeira diferença pode estar.

No entanto, a interpretação correta do intervalo de confiança costuma ser mal compreendida. Um IC de 95% não significa “95% de chance da diferença estar aqui”. Frequentismo não fala de probabilidade sobre parâmetros — apenas sobre repetições amostrais.

Vamos ilustrar com um caso extremo: comparando 500 mil visitas da versão A (com taxa de 0.3%) com apenas 5.000 visitas da nova versão B.

from statsmodels.stats.proportion import confint_proportions_2indep

ci_low, ci_high = confint_proportions_2indep(
    count1=1441, nobs1=500000,  # A
    count2=19, nobs2=5000,      # B
    method='wald'
)
print(f"IC 95% da diferença B - A: {ci_low:.4%} a {ci_high:.4%}")
# IC 95%: -0.2630% a 0.0794%

O intervalo inclui zero. Isso quer dizer que, se repetíssemos esse experimento diversas vezes, 95% dos intervalos construídos dessa forma conteriam a diferença real — que pode ser positiva, negativa ou nula.

Ele também inclui valores positivos — o que mostra que, mesmo com a incerteza, não podemos ignorar a possibilidade de que a nova versão seja melhor.

O problema aqui não é o método, mas o que ele não responde. O intervalo nos diz onde poderia estar a diferença. Mas não diz quão provável é que essa diferença seja positiva.

Se estamos em um dilema de produto, a pergunta prática não é "o intervalo inclui zero?", mas sim:

→ Dado o que observamos, qual a chance de que a nova versão seja de fato melhor?

Para isso, precisamos de uma abordagem que modele diretamente a incerteza. E é aí que o bayesianismo brilha.

Bayesianismo: Incerteza como Objeto de Estudo

O raciocínio bayesiano começa com uma premissa simples, mas poderosa:

A taxa de conversão é um parâmetro fixo, mas desconhecido. O bayesianismo modela nossa incerteza sobre ela como uma variável aleatória.

Em vez de estimar um ponto ou intervalo, passamos a construir uma distribuição de probabilidade sobre o parâmetro. Essa distribuição é atualizada com os dados observados, usando o Teorema de Bayes.

Para taxas de conversão (proporções entre 0 e 1), a escolha natural é a distribuição Beta, conjugada da binomial.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta

# Priori não informativa para ambas as páginas
alpha_prior = 1
beta_prior = 1

# Posterior A e B
alpha_A = alpha_prior + conversoes_A
beta_A = beta_prior + visitors_A - conversoes_A

alpha_B = alpha_prior + conversoes_B
beta_B = beta_prior + visitors_B - conversoes_B

# Plotando as distribuições posteriores e priori
x = np.linspace(0, 0.02, 1000)
plt.figure(figsize=(10,6))
plt.plot(x, beta.pdf(x, alpha_prior, beta_prior), '--', label='Priori', alpha=0.5)
plt.plot(x, beta.pdf(x, alpha_A, beta_A), label=f'Posterior A ({conversoes_A}/{visitors_A})')
plt.plot(x, beta.pdf(x, alpha_B, beta_B), label=f'Posterior B ({conversoes_B}/{visitors_B})')
plt.xlabel('Taxa de conversão')
plt.ylabel('Densidade')
plt.title('Distribuições Posteriores e Priori (Bayesianas)')
plt.legend()
plt.show()

Começamos com uma priori não informativa (Beta(1,1), equivalente a uma uniforme entre 0 e 1). Após observar os dados, atualizamos os parâmetros com as conversões e os fracassos.

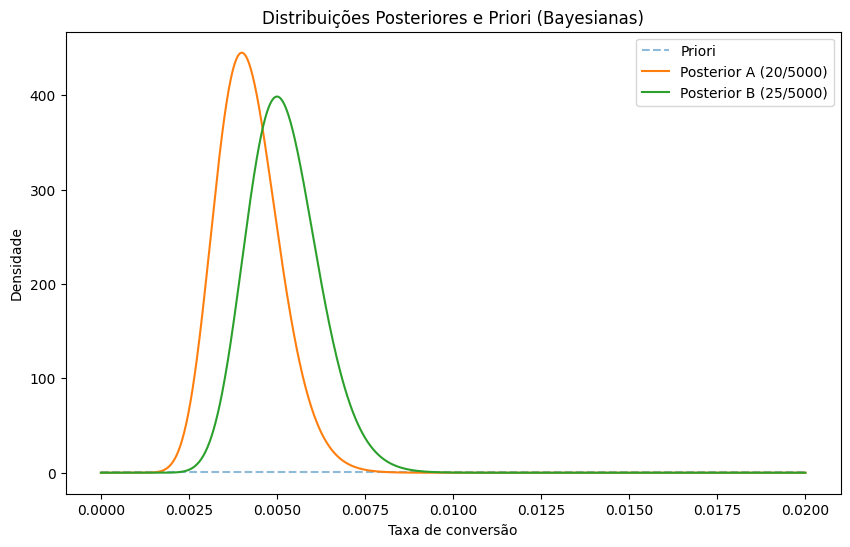
A partir disso, podemos amostrar 100 mil vezes as taxas de conversão plausíveis para A e B, dadas as evidências:

from scipy.stats import beta
import numpy as np

# Amostrando valores das distribuições Beta (posteriores)
samples_A = np.random.beta(alpha_A, beta_A, size=100_000)
samples_B = np.random.beta(alpha_B, beta_B, size=100_000)

Agora temos distribuições completas para nossas crenças sobre as taxas de conversão de A e B. E a diferença entre elas também pode ser tratada como uma distribuição inferida — com média, variância e densidade.

diff = samples_B - samples_A

É essa diferença que importa: o quanto a nova versão supera (ou não) a atual — e com que confiança podemos afirmar isso.

Resultados: Probabilidade, Não Ponto de Corte

Uma das perguntas mais naturais é:

→ “Qual a chance da nova versão ser melhor que a antiga?”

E com a abordagem bayesiana, a resposta é direta:

prob_B_melhor = np.mean(samples_B > samples_A)

Probabilidade de B > A: 77.11%

Isso quer dizer que, com base nos dados e na modelagem que usamos, acreditamos com 77% de confiança que a versão B é melhor que a versão A.

Ao invés de aceitar ou rejeitar, atribuímos probabilidade. Isso permite decisões graduais, ponderadas com base em risco e recompensa. Podemos até definir políticas de rollout do tipo:

• 80% de chance: lançar para todos
• 60–80%: lançar para 10% e monitorar
• <60%: manter controle

Além disso, podemos plotar a distribuição da diferença B - A e observar:

• Um pico à direita de zero
• Uma cauda ainda presente no lado negativo

import matplotlib.pyplot as plt
import seaborn as sns

# Diferença entre as amostras
diff_samples = samples_B - samples_A

# Plotando a distribuição da diferença
plt.figure(figsize=(10, 6))
sns.histplot(diff_samples, bins=100, stat='density', kde=True, color='purple', alpha=0.6)
plt.axvline(0, color='black', linestyle='--', label='B = A')
plt.title('Distribuição da Diferença (B - A) nas taxas de conversão')
plt.xlabel('Diferença na taxa de conversão (θ_B - θ_A)')
plt.ylabel('Densidade')
plt.legend()
plt.show()

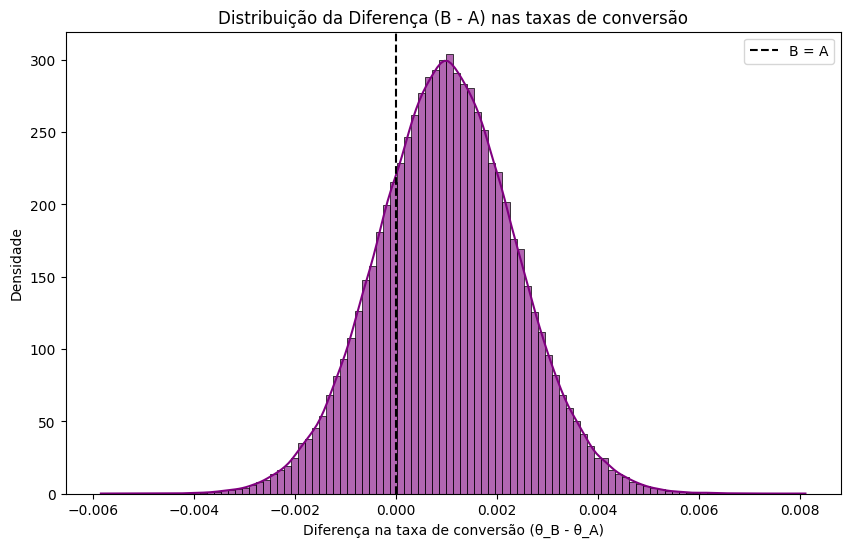
A densidade maior está no lado positivo. Ainda há incerteza — mas agora ela tem forma, volume e sentido.

Priori Informada: Incorporando Histórico

E se a versão A tiver histórico? Simulamos 50.000 visitas anteriores com taxa de 0.3%, e usamos isso como base da distribuição Beta:

historical = 50000

historical_conversion_A = taxa_A * historical

historical_not_conversion_A = historical - historical_conversion_A

print(historical_conversion_A)
print(historical_not_conversion_A)

# 150.0
# 49850.0

from scipy.stats import beta
import numpy as np
import matplotlib.pyplot as plt

# A tem histórico
alpha_prior = historical_conversion_A
beta_prior = historical_not_conversion_A

print(f"Taxa de conversão A: {alpha_prior / (alpha_prior + beta_prior)}")

# Posterior A e B
alpha_A = alpha_prior + conversoes_A
beta_A = beta_prior + visitors_A - conversoes_A

alpha_B = alpha_prior + conversoes_B
beta_B = beta_prior + visitors_B - conversoes_B

# Plotando as distribuições posteriores e priori
x = np.linspace(0, 0.02, 1000)
plt.figure(figsize=(10,6))
plt.plot(x, beta.pdf(x, alpha_prior, beta_prior), '--', label='Distribuição Priori', color='gray')
plt.plot(x, beta.pdf(x, alpha_A, beta_A), label=f'Posterior A ({conversoes_A}/{visitors_A})')
plt.plot(x, beta.pdf(x, alpha_B, beta_B), label=f'Posterior B ({conversoes_B}/{visitors_B})')
plt.xlabel('Taxa de conversão')
plt.ylabel('Densidade')
plt.title('Distribuições Posteriores (Bayesianas)')
plt.legend()
plt.show()

Isso fortalece a confiança em A — e exige que B ofereça evidência mais robusta para superá-la.

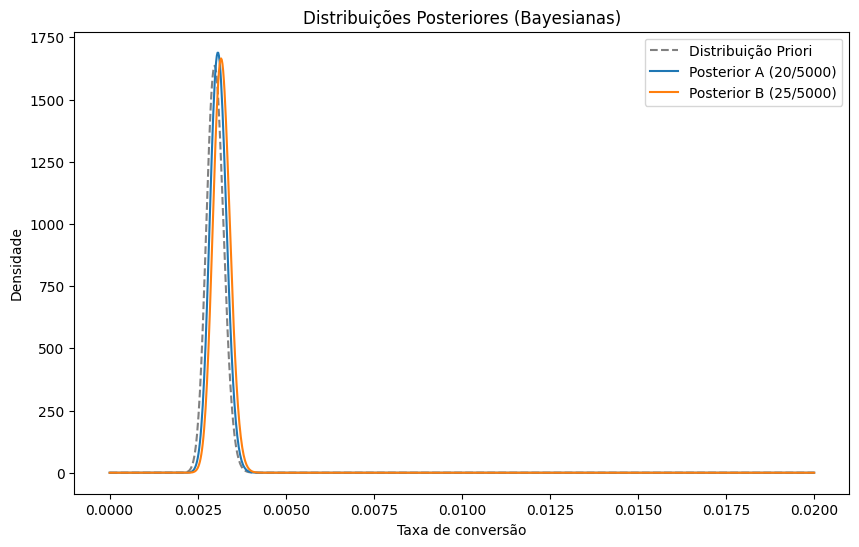
Com as distribuições atualizadas, a probabilidade de B vencer A cai:

from scipy.stats import beta
import numpy as np

# Amostrando valores das distribuições Beta (posteriores)
samples_A = np.random.beta(alpha_A, beta_A, size=100_000)
samples_B = np.random.beta(alpha_B, beta_B, size=100_000)

# Comparando: em quantos casos B > A
prob_B_melhor = np.mean(samples_B > samples_A)

# Resultado
print(f"Probabilidade de que B tenha maior taxa de conversão que A: {prob_B_melhor:.2%}")

Probabilidade de B > A: 60.58%

Em contextos conservadores, talvez isso ainda não seja o bastante. Mas a mensagem do modelo é clara: ainda há incerteza, mas estamos caminhando.

Assimetria de Priori: Um Modelo Mais Realista

No mundo real, B é novidade. A é o padrão, testado e aprovado. Refletimos isso no modelo: A recebe uma prior informada, B começa com Beta(1,1). Resultado:

• A distribuição de A é estreita e centrada.
• A de B é larga e mais incerta.
• A diferença entre elas ganha novo significado: não basta B ter mais conversões — é preciso vencer o histórico.

from scipy.stats import beta
import numpy as np
import matplotlib.pyplot as plt

# A tem histórico
alpha_prior_A = historical_conversion_A
beta_prior_A = historical_not_conversion_A

# B é novo
alpha_prior_B = 1
beta_prior_B = 1


print(f"Taxa de conversão A: {alpha_prior_A / (alpha_prior_A + beta_prior_A)}")
print(f"Taxa de conversão B: {alpha_prior_B / (alpha_prior_B + beta_prior_B)}")

# Posterior A e B
alpha_A = alpha_prior_A + conversoes_A
beta_A = beta_prior_A + visitors_A - conversoes_A

alpha_B = alpha_prior_B + conversoes_B
beta_B = beta_prior_B + visitors_B - conversoes_B

# Plotando as distribuições posteriores e priori
x = np.linspace(0, 0.02, 1000)
plt.figure(figsize=(10,6))
plt.plot(x, beta.pdf(x, alpha_prior_A, beta_prior_A), '--', label='Distribuição Priori', color='gray')
plt.plot(x, beta.pdf(x, alpha_prior_B, beta_prior_B), '--', label='Distribuição Priori', color='gray')
plt.plot(x, beta.pdf(x, alpha_A, beta_A), label=f'Posterior A ({conversoes_A}/{visitors_A})')
plt.plot(x, beta.pdf(x, alpha_B, beta_B), label=f'Posterior B ({conversoes_B}/{visitors_B})')
plt.xlabel('Taxa de conversão')
plt.ylabel('Densidade')
plt.title('Distribuições Posteriores (Bayesianas)')
plt.legend()
plt.show()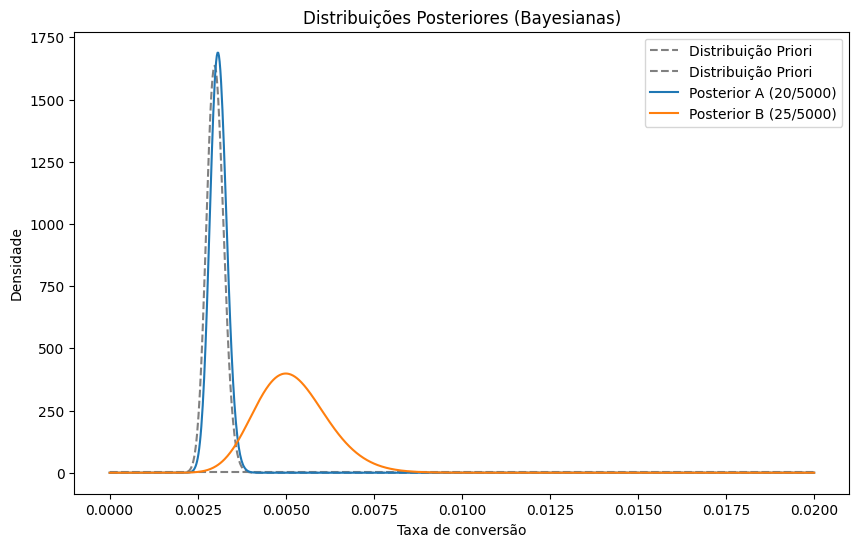

Assim, com os dados atuais, o modelo nos dá:

from scipy.stats import beta
import numpy as np

# Amostrando valores das distribuições Beta (posteriores)
samples_A = np.random.beta(alpha_A, beta_A, size=100_000)
samples_B = np.random.beta(alpha_B, beta_B, size=100_000)

# Comparando: em quantos casos B > A
prob_B_melhor = np.mean(samples_B > samples_A)

# Resultado
print(f"Probabilidade de que B tenha maior taxa de conversão que A: {prob_B_melhor:.2%}")

Probabilidade de B > A: 98.89%
Intervalo de credibilidade (B - A): 0.0250% a 0.4319%

Ou seja: evidência forte. A totalidade do intervalo está acima de zero. Mesmo com dados escassos e priori conservadora, a vantagem de B parece real e consistente.

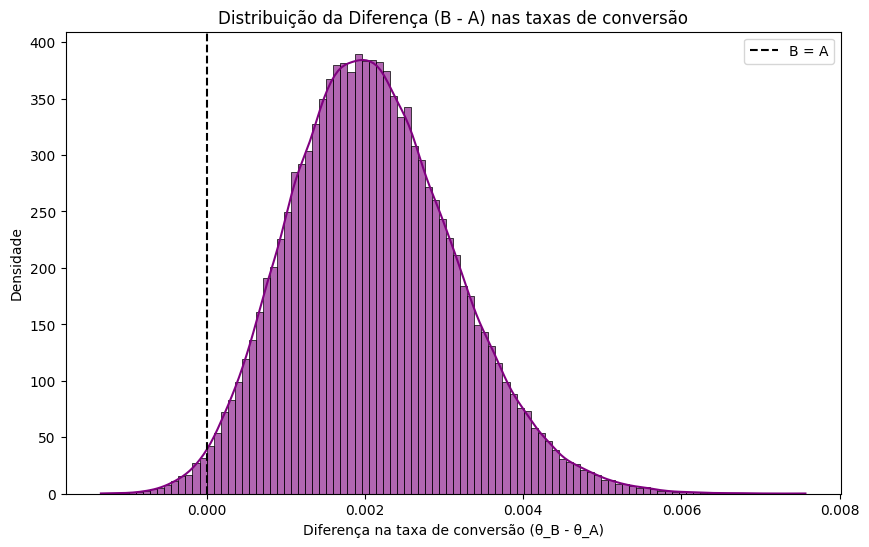
Conclusão: A Incerteza Como Ferramenta

Testes A/B com conversões baixas são traiçoeiros. À primeira vista, parecem simples: dois grupos, duas taxas, um p-valor. Mas sob a superfície, o que temos é um terreno instável — onde decisões de produto, marketing ou negócio podem ser tomadas com base em ruído.

O frequentismo nos oferece uma estrutura de decisão baseada em rejeição ou não rejeição de hipóteses, útil em muitos contextos. Mas quando lidamos com incertezas sutis e decisões graduais, a abordagem bayesiana permite modelar nuances com mais flexibilidade.

O bayesianismo não traz certezas absolutas. Mas nos oferece algo mais precioso: a forma da incerteza. Em vez de perguntar “isso é significativo?”, passamos a perguntar:

→ “Dado o que sei, qual a probabilidade de que essa mudança melhore meu produto?”
→ “Com quanta confiança posso apostar nisso?”
→ “Vale o risco agora — ou espero mais dados?”

Modelar explicitamente a incerteza, incorporar conhecimento prévio, reconhecer assimetrias — tudo isso aproxima a estatística da realidade prática. Ela deixa de ser um veredito mecânico e se torna uma ferramenta estratégica: nos ajuda a raciocinar sobre incerteza, incorporar experiência e tomar decisões mais conscientes — mesmo quando os dados ainda não gritam.

Em tempos onde decisões rápidas valem milhões, talvez a melhor resposta não seja um "sim" ou "não". Mas um "depende — e aqui está o porquê".