Explorando Embeddings do GPT para Classificação de Sentimentos em Tweets

Decidi quebrar o gelo com a API da OpenAI e decidi começar com a funcionalidade de embeddings usando o GPT. Nesse artigo vamos construir um classificador bem simples no melhor estilo POC a partir de um dataset para análise de sentimentos que encontrei no kaggle.

Para começar, fiz alguns ajustes no dataset:

1. Troquei o nome das colunas
2. Mantive somente sentimentos positivos ou negativos, removendo os neutros
3. Removi linhas sem texto
4. Ajustei o label para ser 1 para Positivo e 0 para Negativo (originalmente era 1 e -1)
5. Obtive um sample de 10k linhas (para agilizar o processo)

import pandas as pd

training_df = pd.read_csv('Twitter_Data.csv')
training_df.columns = ['text', 'label']

training_df = training_df[training_df['label'].isin([-1, 1])]

training_df = training_df[~training_df['text'].isnull()]

training_df['label'] = (training_df['label'] == 1.0).astype(float)

training_df = training_df.sample(10000)

training_df.head()

Embeddings com GPT

Com o dataset ajustado, utilizei a API da OpenAI para obter embeddings para esses tweets. Você precisará substituir API_KEY com sua key da OpenAI. Caso você não tenha, basta acessar a documentação da API, criar sua conta e gerar sua key (link da documentação).

Apesar de ser uma API paga, eu gerei o embedding de somente 10k linhas, o que me gerou um custo menor que $ 0.02. Lembrando que o objetivo desse post é ser uma POC, então meu objetivo foi gastar o mínimo possível.

Em posse da API_KEY, basta utilizar a API da OpenAI para obter os embeddings dos tweets. Esses embeddings terão tamanho 1536.

from openai import OpenAI
from tqdm import tqdm

tqdm.pandas()
client = OpenAI(api_key=API_KEY)

def get_embedding(text, model="text-embedding-3-small"):
   text = text.replace("\n", " ")
   return client.embeddings.create(input = [text], model=model).data[0].embedding

training_df['ada_embedding'] = training_df.text.progress_apply(lambda x: get_embedding(x, model='text-embedding-3-small'))
training_df.to_csv('output/embedded_10k_tweets.csv', index=False)

Redução de Dimensionalidade com PCA

Como 1536 é um número muito grande de dimensões para esse dataset de somente 10k linhas, decidi usar PCA para reduzir essas dimensões para um número arbitrário significativamente menor, mais especificamente 15 dimensões.

import numpy as np
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split

train_df, test_df = train_test_split(training_df, test_size=0.2)

n_components = 15
pca = PCA(n_components=n_components)

embeddings_train = np.stack(train_df['ada_embedding'].values)
embeddings_test = np.stack(test_df['ada_embedding'].values)

pca.fit(embeddings_train)

reduced_embeddings_train = pca.transform(embeddings_train)
reduced_embeddings_test = pca.transform(embeddings_test)

train_df['pca_embeddings'] = list(reduced_embeddings_train)
test_df['pca_embeddings'] = list(reduced_embeddings_test)

for i in range(reduced_embeddings_train.shape[1]):
    train_df[f'pca_{i+1}'] = reduced_embeddings_train[:, i]
    test_df[f'pca_{i+1}'] = reduced_embeddings_test[:, i]

Grafo com os Tweets

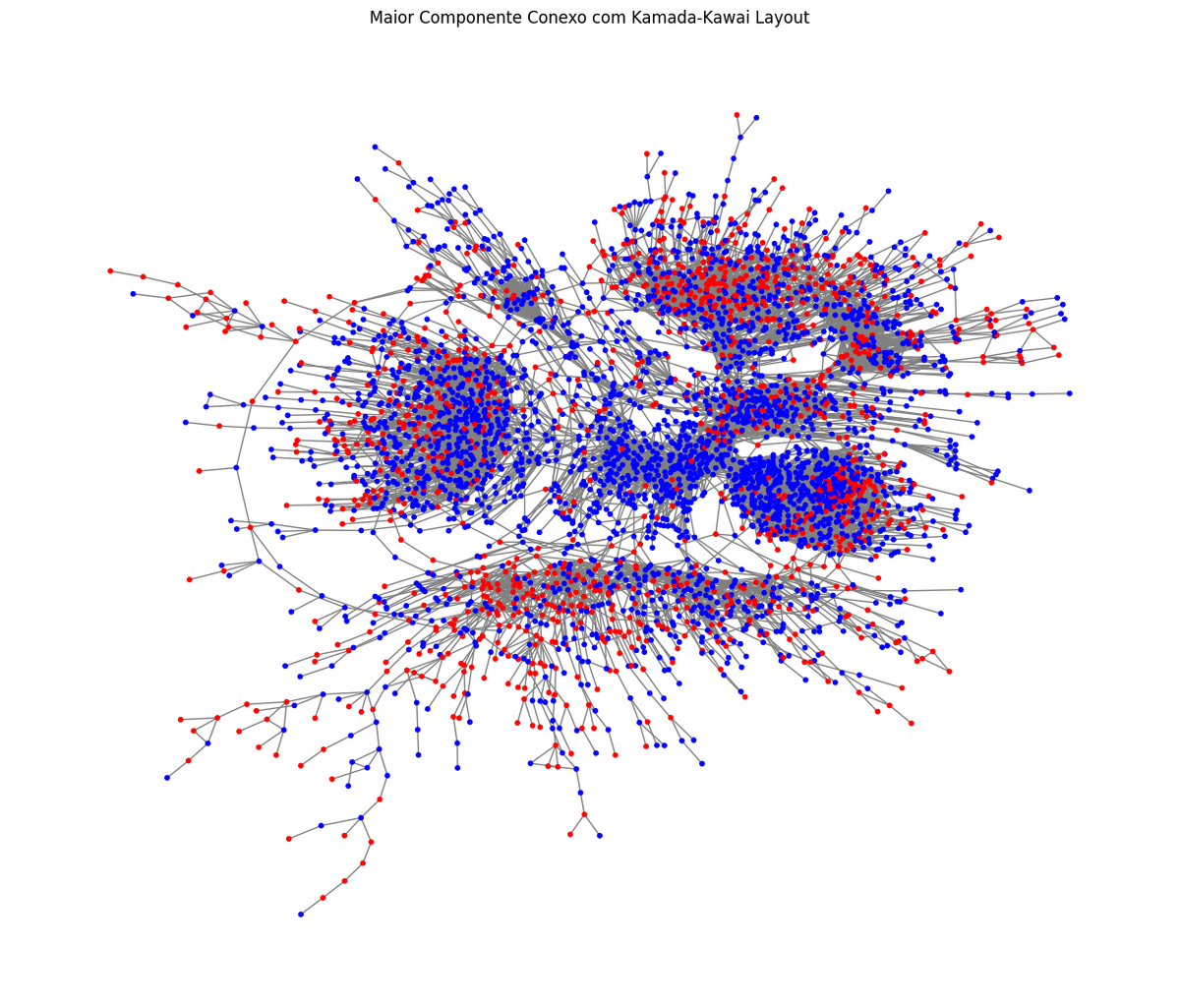
Antes de continuar com o classificador, vou criar uma visualização diferente para esses dados na forma de um grafo. Usei a biblioteca networkx para construir um grafo em que cada tweet é vértice e dois vértices estão conectados se são similares o suficiente.

Para definir as arestas, calculei a similaridade de cossenos dos embeddings reduzidos com o PCA e conectei vértices com similaridade maior que 0.85. Isso me gerou um grafo com 8k vértices e ~24k arestas.

from sklearn.metrics.pairwise import cosine_similarity
import networkx as nx

similarity_matrix = cosine_similarity(train_df['pca_embeddings'].tolist())

G = nx.Graph()

for index, row in train_df.iterrows():
    G.add_node(row['text'], label=row['label'])

threshold = 0.8

for i in range(0, len(similarity_matrix)):
    for j in range(i+1, len(similarity_matrix)):
        if similarity_matrix[i][j] > threshold:
            G.add_edge(
                train_df.iloc[i]['text'],
                train_df.iloc[j]['text'],
                weight=similarity_matrix[i][j]
            )

Para visualizar esse grafo vou extrair somente o maior componente conexo. Não usei esse grafo para nada além desse plot nesse post, mas uma sugestão é aproveitar essa estrutura do grafo para extrair outras features para o classificador, como medidas de grau, centralidade, etc.

import matplotlib.pyplot as plt

components = list(nx.connected_components(G))

largest_component = max(components, key=len)

S = G.subgraph(largest_component)

node_colors = ['blue' if S.nodes[node].get('label') == 1 else 'red' for node in S.nodes()]
pos = nx.kamada_kawai_layout(S)

plt.figure(figsize=(12, 10))
nx.draw(S, pos, with_labels=False, node_color=node_colors, edge_color='gray', 
        node_size=10, font_weight='bold')
plt.title('Maior Componente Conexo com Kamada-Kawai Layout')
plt.show()

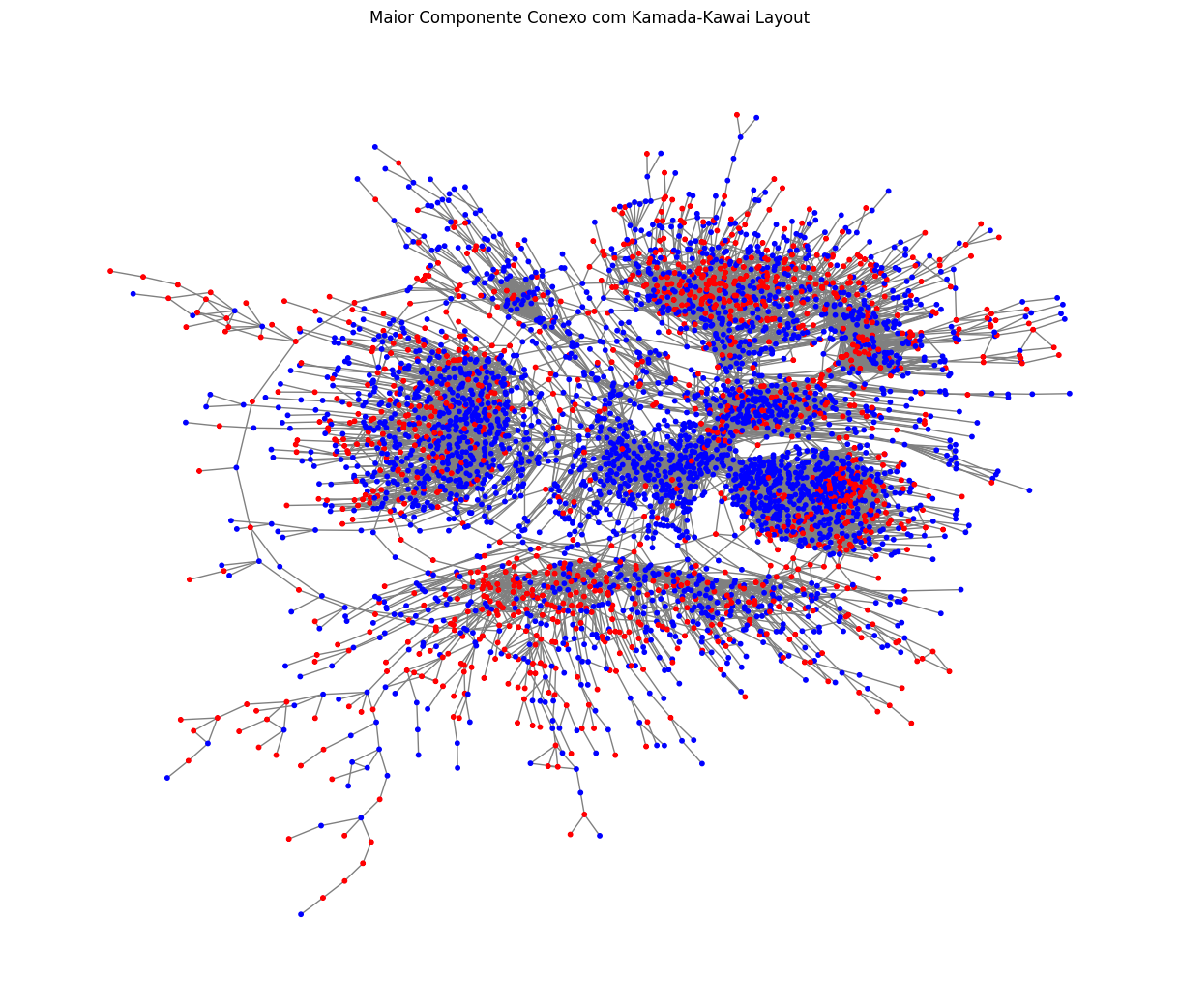
Note que até é possível ver que alguns nós com sentimento positivo estão mais próximos entre si, provavelmente uma análise da estrutura de comunidades dessa rede poderia revelar alguns insights adicionais.

Classificador de Sentimentos

Retomando ao classificador, vou utilizar cada uma das 15 dimensões do PCA como uma feature para construir uma regressão logística. Vou pular toda a etapa de feature engineering nesse post, mas é uma sugestão caso queira ir mais a fundo na construção do classificador. Também não testei outros tipos de modelo.

Usei a biblioteca statsmodels para construir a regressão com as 15 features obtidas do PCA. Vale notar no sumário como algumas dimensões do PCA, como a 10 e 11, tem um P-value alto. Isso sugere que poderíamos aplicar um processo de feature selection para reduzir o set de features e eventualmente melhorar a performance do classificador. Vou pular essa etapa nesse POC, mas também deixo como sugestão.

import numpy as np
import statsmodels.api as sm

features = [f'pca_{i}' for i in range(1, n_components+1)]

print(features)

X_train = train_df[features]
X_test = test_df[features]
y_train = train_df["label"]
y_test = test_df["label"]

X_train_sm = sm.add_constant(X_train)

model = sm.Logit(y_train, X_train_sm)

result = model.fit()

result.summary().tables[1]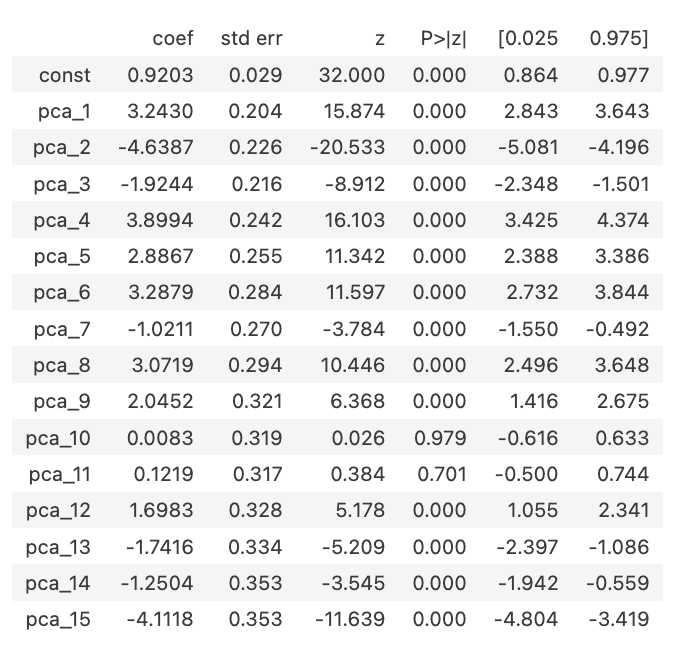

Calculando o AUC dessa regressão obtemos um valor de 0.738, o que não é nem bom e nem ruim. Considerando que pulamos diversas etapas de otimização e não exploramos features adicionais, considero uma performance satisfatória.

from sklearn.metrics import roc_curve, roc_auc_score

X_test_sm = sm.add_constant(X_test)

probs = result.predict(X_test_sm)


fpr, tpr, thresholds = roc_curve(y_test, probs)

auc_score = roc_auc_score(y_test, probs)

plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {auc_score:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc='lower right')
plt.grid(True)
plt.show()

print(auc_score)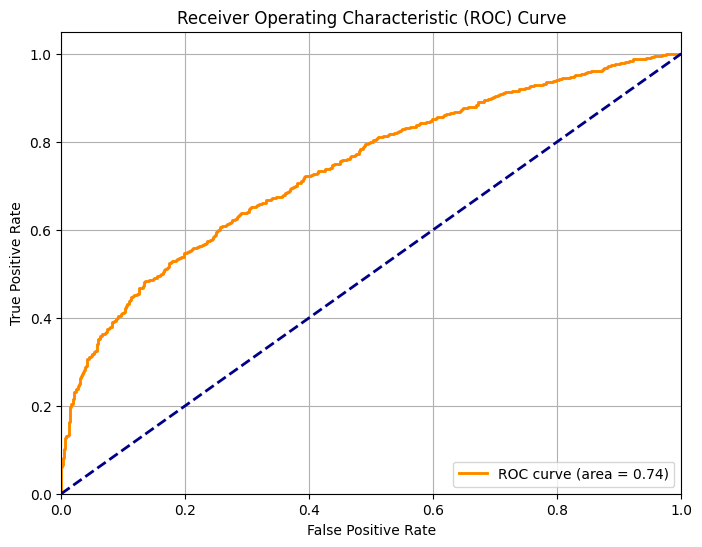

Plotando a matriz de confusão podemos notar que a predição dos verdadeiros negativos é boa, mas considerando os falso negativos é bem ruim. Poderíamos eventualmente ajustar o threshold para ponderar melhor, mas não é o objetivo nesse post.

from sklearn.metrics import ConfusionMatrixDisplay, confusion_matrix

optimal_idx = np.argmax(tpr - fpr)
optimal_threshold = thresholds[optimal_idx]

print(f'Optimal threshold: {optimal_threshold}')

y_pred_optimal = np.where(probs >= optimal_threshold, 1, 0)

def plot_confusion_matrix(y_preds, y_true):
    cm = confusion_matrix(y_true, y_preds, normalize="true")
    fig, ax = plt.subplots(figsize=(6, 6))
    disp = ConfusionMatrixDisplay(confusion_matrix=cm)
    disp.plot(cmap="Blues", values_format=".2f", ax=ax, colorbar=False)
    plt.title("Normalized confusion matrix")
    plt.show()
    
plot_confusion_matrix(y_pred_optimal, y_test)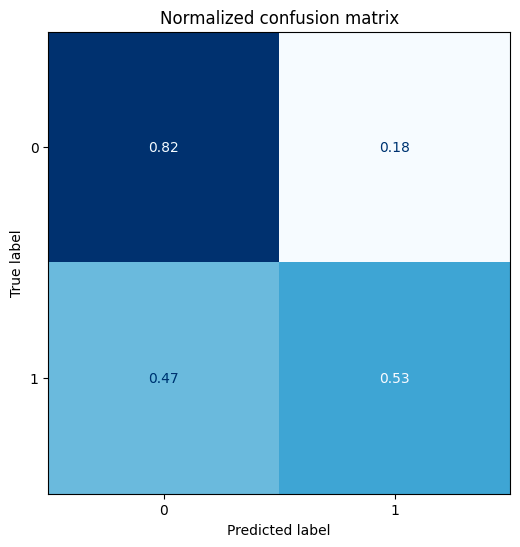

Visualização Tri-Dimensional

Para encerrar minha exploração desses embeddings, construi um plot tri-dimensional para visualizar os tweets segmentados pelos sentimentos. Apesar de ser uma visualização simples, é possível notar uma certa distinção espacial dos sentimentos.

from sklearn.manifold import TSNE
from mpl_toolkits.mplot3d import Axes3D

tsne = TSNE(n_components=3, perplexity=15, random_state=42, init="random", learning_rate=20)
vis_dims2 = tsne.fit_transform(matrix)

x = vis_dims2[:, 0]
y = vis_dims2[:, 1]
z = vis_dims2[:, 2]

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

colors = ['red' if label == 0 else 'blue' for label in train_df['label']]

ax.scatter(x, y, z, color=colors, alpha=0.1)

ax.set_title("Visualização 3D usando t-SNE")
ax.set_xlabel("Componente 1")
ax.set_ylabel("Componente 2")
ax.set_zlabel("Componente 3")

plt.show()

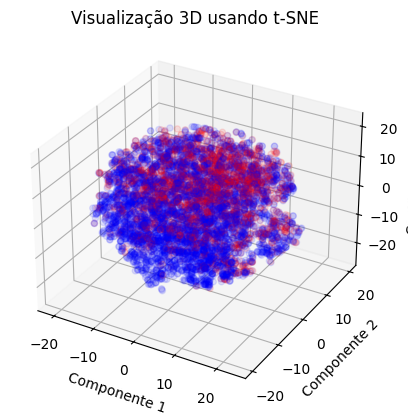
Conclusões

Meu objetivo era explorar o uso dos embeddings obtidos com a API da OpenAI e, de modo geral, achei bem interessante. Gastei cerca de $0.01 para obter os embeddings de 10k tweets, o que considero um custo aceitável. Por ser acessível e fácil de usar, é possível usar essa API de embeddings como uma forma rápida de construir um protótipo de um modelo ou aplicação.

Dentre as opções que vejo como interessantes nesse cenário dos tweets, é possível:

1. Construir um grafo usando alguma métrica de distância a partir dos embeddings ou de um embedding dimensionalmente reduzido. Extrair features para um classificador a partir dessa grafo ou até mesmo usar a estrutura do grafo como classificador.
2. Treinar um modelo supervisionado para classificação usando os embeddings para gerar features com algum método de redução de dimensionalidade. Se o conjunto for grande o suficiente, pode-se usar até mesmo todas as dimensões do embedding com algum método de feature selection.

Nos vemos na próxima! 😃