Um exercício sobre Inferência Causal: qual o impacto do treinamento no salário dos funcionários?

Neste post, exploraremos conceitos de inferência causal utilizando dados simulados e técnicas de regressão linear para quantificar o impacto de um treinamento no salário dos funcionários. Será que o treinamento é responsável por um aumento salarial? Quanto do aumento salarial é explicado pelo treinamento?

Esse será um exercício com dados simulados e não representa uma situação real, o objetivo é explorar e entender melhor os conceitos de inferência causal.

Análise

Primeiramente, vamos gerar uma população aleatória de 1000 funcionários cuja idade está entre 20 e 60 anos. A idade dessa população vai seguir uma distribuição uniforme. Além da idade, geramos uma métrica de experiência e outra de engajamento, ambas fictícias e que variam entre 0 e 1, para indicar quão experimente e engajado é o funcionário.

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sm
import statsmodels.formula.api as smf


np.random.seed(42)

n = 1000  # Número de funcionários

# Gerando dados simulados
idade = np.random.randint(20, 60, size=n)
experiencia = np.random.random(size=n)
engajamento = np.random.random(size=n)

plt.figure(figsize=(18, 5))

# Plot para Idade
plt.subplot(1, 3, 1) 
sns.kdeplot(idade, shade=True)
plt.title('Distribuição da Idade')

# Plot para Experiência
plt.subplot(1, 3, 2)
sns.kdeplot(experiencia, shade=True, color='orange')
plt.title('Distribuição da Experiência')

# Plot para Engajamento
plt.subplot(1, 3, 3)
sns.kdeplot(engajamento, shade=True, color='green')
plt.title('Distribuição do Engajamento')

plt.tight_layout() 
plt.show()

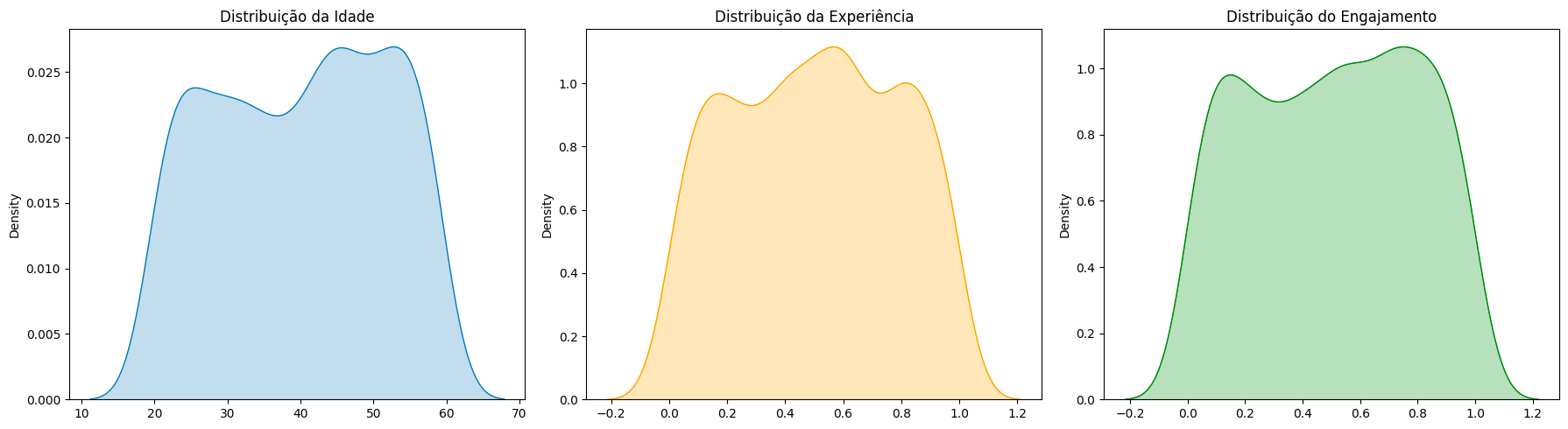
Analisando de forma intuitiva, isso significa que temos uma população com idades, experiências e níveis de engajamento variados. Até aqui, não existe nenhuma relação entre essas variáveis pois todas foram geradas aleatoriamente para seguir uma distribuição normal.

Em seguida, vou gerar uma distribuição binomial para representar quais funcionários participaram ou não do treinamento. Novamente, vou gerar uma distribuição aleatória e independente das demais variáveis criadas até aqui.

No meu caso, gerou uma média de 50.8%. Esse número pode variar para você. Isso significa que 50.8% dos funcionários participaram do treinamento, aproximadamente metade.

participou_treinamento = np.random.binomial(1, 0.5, size=n)

print(np.mean(participou_treinamento))

Ou seja, temos uma população com 3 características bem distribuídas em que 50% participou do treinamento. Embora isso seja um exemplo fictício com dados sintéticos, é uma representação de algo que poderia acontecer na realidade.

O próximo passo é definir o salário desses funcionários antes do treinamento. Essa será nossa 4ª característica da população. Ao contrário das demais definidas até aqui, essa não será aleatória. Pelo contrário, irá depender das demais. Intuitivamente, isso significa dizer que o salário dessa população será definido com base na idade, engajamento e experiência dos funcionários. É uma tentativa de simular o que acontece no mundo real.

Nesse caso, o salário será definido por:

1. salário base: R$ 1.000,00
2. experiência: adiciona entre 0 a R$ 2.000,00 no salário
3. idade: adiciona entre R$ 400,00 a 1.200,00 no salário
4. engajamento: adiciona entre 0 a R$ 1.000 no salário
5. aleatoriedade: adiciona entre 0 a R$ 1.000 no salário

Ou seja, o salário de um funcionário pode variar de acordo com todas essas características, mas também existe um fator de aleatoriedade que representa outras variáveis que podem afetar o salário.

salario_antes = 1000 + (2000 * experiencia) + (idade * 20) + (engajamento * 1000) + np.random.normal(0, 1000, size=n)

plt.figure(figsize=(6, 5))

# Plot para Idade
plt.subplot(1, 1, 1) 
sns.kdeplot(salario_antes, shade=True)
plt.title('Distribuição dos Salários')

plt.tight_layout() 
plt.show()

Em seguida, vamos definir o salário dos funcionários após o treinamento. Esse salário será uma consequência do salário anterior acrescido de uma variável que depende da participação no treinamento. Ou seja, se o funcionário tiver participado do treinamento, ele receberá um aumento proporcional ao seu engajamento. Intuitivamente, isso significa que quanto mais engajado for o funcionário, maior será seu aumento após ter participado treinamento. Além disso, ele também receberá um aumento de (0.3 * 1000) independente do seu engajamento, somente por ter participado do treinamento. Finalmente, existe um fator aleatório que representa outros fatores que podem ter causado o aumento de salário.

salario_depois = salario_antes + (participou_treinamento * (0.3 + engajamento) * 1000) + np.random.normal(0, 500, size=n)

plt.figure(figsize=(6, 5))

# Plot para Idade
plt.subplot(1, 1, 1) 
sns.kdeplot(salario_depois, shade=True)
plt.title('Distribuição dos Salários')

plt.tight_layout() 
plt.show()

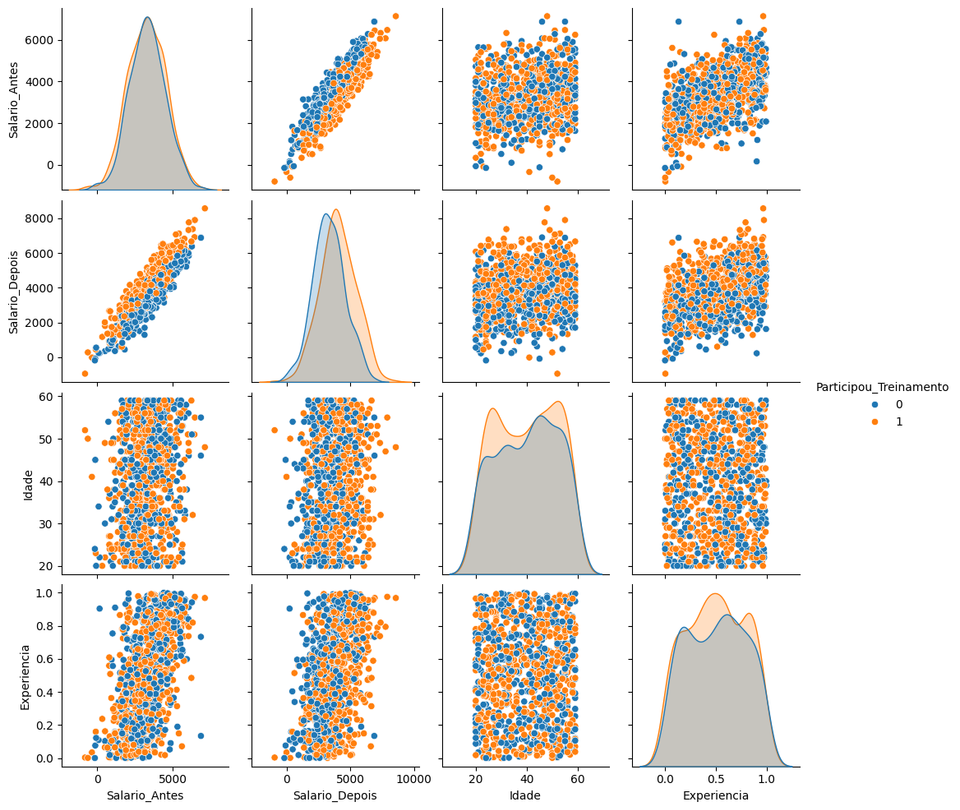
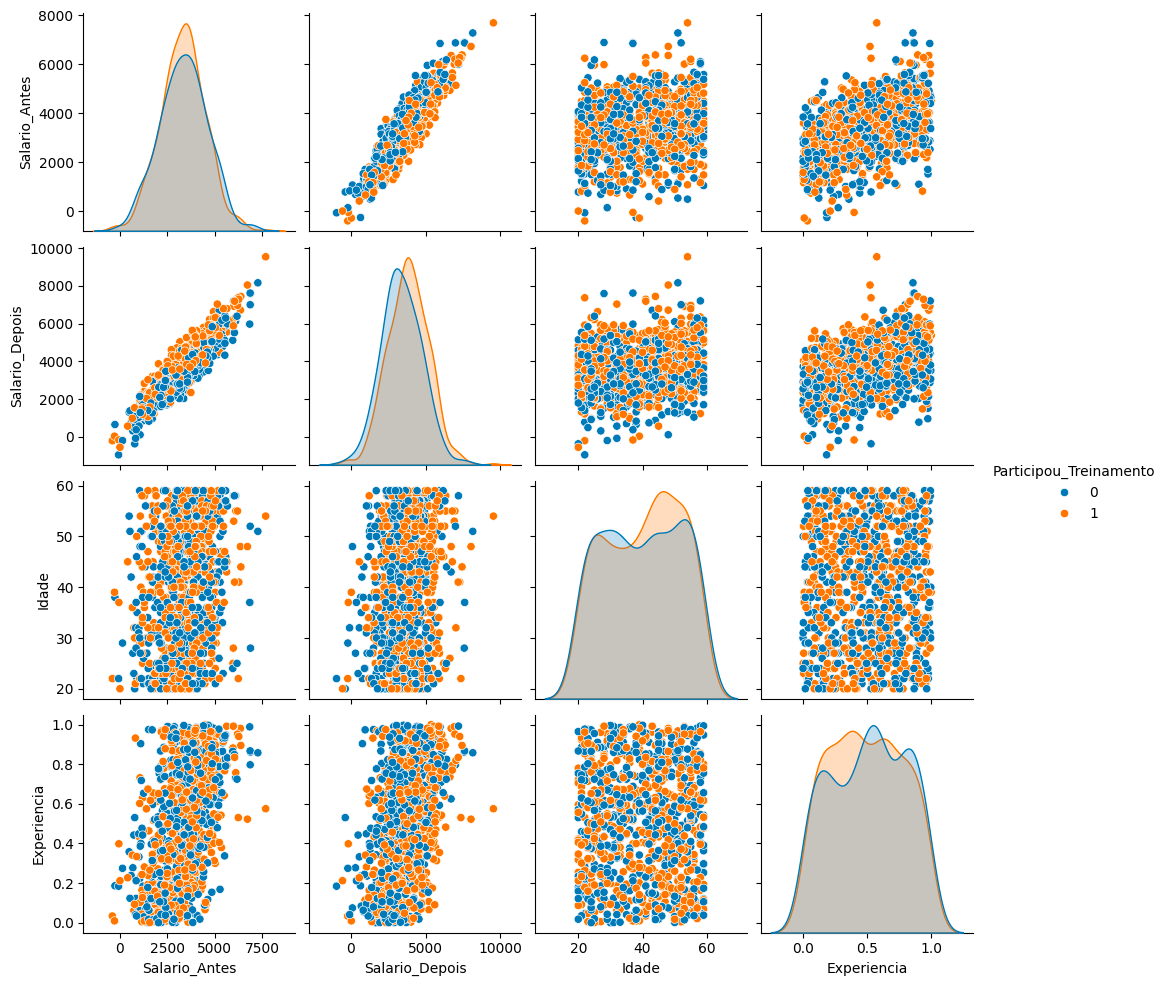
Unificando todos os dados até aqui em um dataframe e comparando as variáveis em um pairplot para visualizar melhor os dados. Observe que as variáveis são bem distribuídas entre quem participou ou não do treinamento.

# Criando o DataFrame
dados = pd.DataFrame({'Idade': idade,
                      'Experiencia': experiencia,
                      'Engajamento': engajamento,
                      'Participou_Treinamento': participou_treinamento,
                      'Salario_Antes': salario_antes,
                      'Salario_Depois': salario_depois})

sns.pairplot(dados[['Salario_Antes', 'Salario_Depois', 'Idade', 'Experiencia', 'Participou_Treinamento']], hue='Participou_Treinamento')
plt.show()

Vamos fazer agora o exercício de imaginar que não sabemos o critério que definiu o salário após o treinamento. Ou seja, conhecemos todas as variáveis, mas não sabemos a fórmula exatamente que definiu o salário após o treinamento. Vamos começar analisando a relação entre o novo salário dos funcionários e somente o fato de terem participado ou não do treinamento.

modelo = smf.ols('Salario_Depois ~ Participou_Treinamento', data=dados).fit()
print(modelo.summary().tables[1])

sns.boxplot(data=dados, x='Participou_Treinamento', y='Salario_Depois')

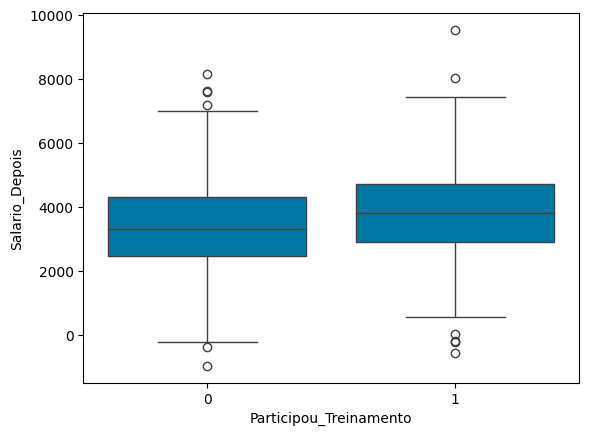
Analisando esses dados, notamos que ambos tem p-value < 0.05, ou seja, são bons discriminantes do novo salário. Além disso, o Intercepto está em R$ 3.389. Isso significa o salário base da população. Além disso, a variável Participou_Treinamento tem coeficiente R$ 449. Isso significa que, quem participou do treinamento, tem um salário R$ 449 maior.

Se você analisar o boxplot, irá notar que, de fato, o salário de quem participou do treinamento é, de fato, maior. Mas isso faz sentido?

De certa forma faz, afinal, quem participou do treinamento tem um salário maior. Por outro lado, o salário base não faz tanto sentido assim. Se você lembrar de como definimos o salário, o salário base era R$ 1.000. O que aconteceu aqui é que existem vieses entre quem participou do treinamento, e um deles é o engajamento. Ou seja, o novo salário não depende somente de ter participado do treinamento, mas também do engajamento desse funcionário.

Essa variável (engajamento) é uma cofounder. Ela afeta o resultado final. Vamos incluir ela em nossa análise e verificar como o resultado é modificado. Eu incluo ela multiplicando a variável Participou_Treinamento assumindo a premissa de que, quanto mais engajado o funcionário, mais proveitoso será o treinamento para ele.

modelo = smf.ols('Salario_Depois ~ Participou_Treinamento * Engajamento', data=dados).fit()
print(modelo.summary().tables[1])

sns.scatterplot(data=dados, x='Salario_Antes', y='Salario_Depois', hue='Participou_Treinamento')

Perceba que agora o valor do intercepto caiu para cerca de R$ 2660, ou seja, o salário base é reduzido. Além disso, o coeficiente da variável Participou_Treinamento caiu de 449 para 387. Isso significa que o fato de ter participado do treinamento teve seu peso reduzido na definição do novo salário.

Por outro lado, a variável Engajamento tem peso 1370. Ou seja, um funcionário com engajamento 1 tem salário R$ 1370 maior que um funcionário com engajamento 0. Por fim, a interação entre Engajamento e Participou_Treinamento tem peso 721. Ou seja, um funcionário que participou do treinamento e tem engajamento 1 tem salário R$ 721,00 maior. Caso o engajamento desse mesmo funcionário fosse 0.5, seu salário seria R$ 360 maior. Ou seja, quanto maior o engajamento dos funcionários que participaram do treinamento, maior será o salário deles.

Poderíamos parar por aqui. Entretanto, temos uma outra variável disponível que ainda não usamos e sabemos que afeta o novo salário: o salário antigo. Perceba que, ao inserir o salário antigo no modelo, a variável Engajamento é fortemente afetada. Seu coeficiente é drasticamente reduzido enquanto seu p-value aumenta.

modelo = smf.ols('Salario_Depois ~ Participou_Treinamento * Engajamento + Salario_Antes', data=dados).fit()
print(modelo.summary().tables[1])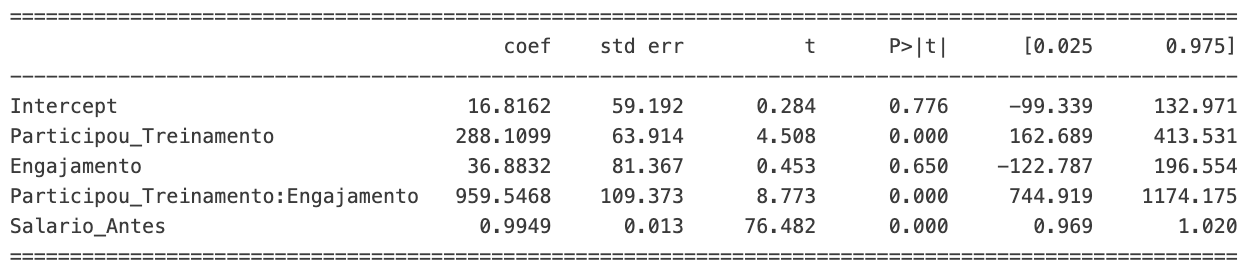

Esse é um indício de que ela perdeu poder preditivo no modelo. Note que, se isso aconteceu após inserir a nova variável Salario_Antes , provavelmente essa nova variável tem correlação com Engajamento. Ou seja, Salario_Antes está, provavelmente, prevendo Engajamento. Ou vice versa.

Uma forma de verificar se isso é ver o quanto de Engajamento é explicado por Salario_Antes. E é possível fazer isso usando uma regressão. Note que o p-value de Engajamento para explicar Salario_Antes é 0. Ou seja, nossa hipótese é verdadeira.

modelo_debias = smf.ols('Salario_Antes ~ Engajamento', data=dados).fit()
print(modelo_debias.summary().tables[1])

Uma forma de corrigir isso é, em vez de inserir Salario_Antes no nosso modelo, inserir somente a parte de Salario_Antes que não é explicada por Engajamento. Dessa forma, a variável Engajamento não seria afetada.

Mas... como fazer isso? Note na regressão acima que Salario_Antes é explicado pelo intercepto + Engajamento. Podemos pegar o resíduo desse modelo (Salario_Antes_Res) para obter a parte de Salario_Antes que não foi explicada por Engajamento. Esse resíduo, ao ser aplicado no nosso modelo, não afetaria a variável Engajamento.

modelo = smf.ols(
    "Salario_Depois ~ (Participou_Treinamento * Engajamento) + salario_antes_debiased",
    data=dados.assign(
        salario_antes_debiased=modelo_debias.resid + dados.Salario_Antes.mean()
    ),
).fit()
print(modelo.summary().tables[1])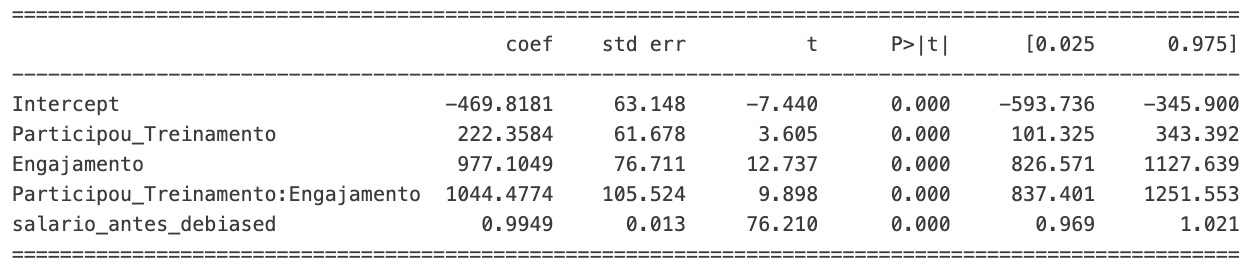

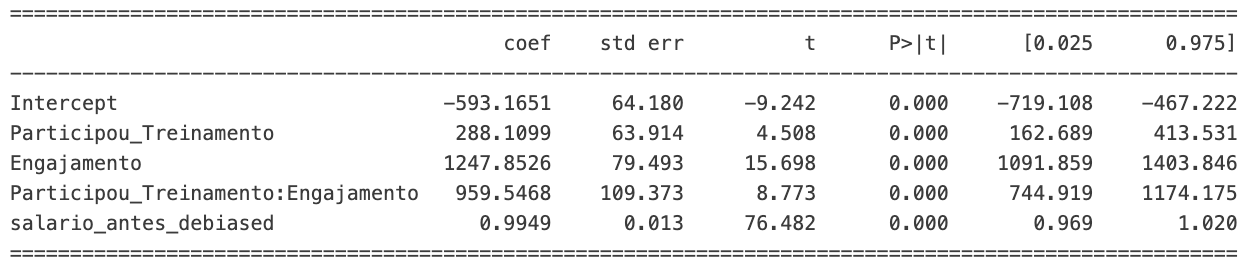
Note que, dessa forma, a variável Engajamento continua com p-value 0. Ou seja, não perdeu seu poder preditivo. Além disso, a variável Salario_Antes (agora salario_antes_debiased) manteve seu coeficiente. Isso faz sentido pois nossas modificações afetaram somente a variável Engajamento.

Em nosso modelo, se um funcionário não participasse do programa de treinamento (Participou_Treinamento = 0), tivesse um nível de engajamento zero (Engajamento = 0), e considerando o ajuste para o salário antes do treinamento através de salario_antes_debiased, esperaríamos, teoricamente, que o salário desse funcionário após o treinamento fosse reduzido em R$ 469 em relação à média ajustada do salário antes do treinamento. Essa é a intuição por trás do intercepto de -469.

Uma forma não exata, mas intuitiva, de entender isso é observar que a média dos salários antes do treinamento é de R$ 3302, enquanto a média dos salários antes do treinamento daqueles que tem engajamento baixo e não participaram do treinamento é de R$ 2723, ou seja, cerca de R$ 600 abaixo. Note que o valor não será exatamente igual ao intercepto pois estou fazendo uma abstração: selecionando usuários com engajamento < 0.05 como se fossem engajamento = 0. Além disso, estou ignorando todas as outras variáveis. Esse é somente um exercício para clarificar o significado do intercepto nesse cenário.

print(dados['Salario_Antes'].mean())
// 3302.832849208488

print(dados.query('Participou_Treinamento == 0 & Engajamento < 0.05')['Salario_Antes'].mean())
// 2723.5835170894634

print(dados.query('Participou_Treinamento == 0 & Engajamento < 0.05')['Salario_Antes'].mean() - dados['Salario_Antes'].mean())
// -579.2493321190245

Finalizando nossas análises, a conclusão final segundo nossa regressão é que:

1. O fato de ter participado do treinamento gera um aumento de salário de cerca de R$ 220.
2. O engajamento tem potencial de gerar um aumento de salário de até R$ 997.
3. O engajamento dos clientes que participaram do treinamento tem potencial para gerar um aumento de até R$ 1044.

Note que definimos o salário após o treinamento como salario_antes + (participou_treinamento * (0.3 + engajamento) * 1000) + np.random.normal(0, 500, size=n). Isso significa que o valor de 220 é próximo o suficiente de (0.3 * 1000). Além disso, o valor 997 é próximo o suficiente de 1000. Isso significa que nossas conclusões estão bem próximas da realidade que foi definida durante a geração dos dados.

Conclusões

Confirmamos que tanto a participação no treinamento quanto o nível de engajamento são fatores significativos que contribuem para um aumento salarial. Além disso, a interação entre essas duas variáveis sugere que o treinamento é mais benéfico para os funcionários altamente engajados, destacando a importância de considerar o engajamento individual ao quantificar o impacto do treinamento. Embora baseado em dados simulados, este exercício ilustra a aplicação da estatística para entender e quantificar o impacto de vieses e de variáveis de tratamento em uma população.

Limitações da Análise

Embora nossa análise tenha explorado o impacto do treinamento e do engajamento no salário dos funcionários, é importante reconhecer que os dados utilizados são completamente simulados. Isso significa que, embora as variáveis e relações imitem situações do mundo real, os dados podem não capturar completamente a complexidade dos cenários reais. Por exemplo, a experiência e o engajamento foram modelados como variáveis contínuas variando uniformemente entre 0 e 1, na vida real essas variáveis podem ter distribuições diferentes.

Além disso, quando definimos o salário após o treinamento com base em uma fórmula específica que inclui o engajamento e a participação no treinamento, assumimos uma relação linear e direta entre essas variáveis. Na prática, o impacto do treinamento no salário pode ser influenciado por uma série de outros fatores não considerados aqui, como a qualidade do treinamento, o campo de atuação do funcionário, o nível hierárquico e a presença de políticas de RH que promovam ou limitem aumentos salariais, etc.

O objetivo do post é expor uma análise inicial utilizando conceitos de inferência causal, ele devem ser vista somente como um ponto de partida para investigações mais profundas e detalhadas, preferencialmente utilizando dados reais.

Indicação de Livro

Se você se interessou pelos conceitos de inferência causal discutidos neste post e deseja aprofundar seus conhecimentos na área, tenho uma recomendação de leitura para você:

Causal Inference in Python
Autor: Matheus Facure

Este livro é uma introdução acessível e prática aos conceitos e técnicas de inferência causal, com exemplos e códigos em Python. O foco está em como aplicar esses métodos para extrair insights causais a partir de dados reais, tornando-o uma leitura interessante para cientistas de dados, pesquisadores e qualquer pessoa interessada em entender os efeitos causais nos dados.