Computação Quântica: colocando o pé na água

Computação Quântica é um tópico que sempre me deixou curioso, mas a única coisa que eu sabia era: na computação quântica, coisas podiam acontecer ao mesmo tempo. Confesso que nunca entendi de forma prática o impacto disso, ai decidi estudar. Embora eu quisesse uma abordagem mais prática para entender o potencial disso tudo e as aplicações que poderiam surgir, só encontrava teoria e mais teoria. Até que isso faz sentido dado o momento atual de conhecimento disso tudo.

Vou logo te avisar: eu queria muito fazer um post prático sobre isso tudo igual eu busquei quando comecei. Mas ainda não cheguei lá. Preciso passar pela teoria primeiro, principalmente porque ainda não existe muita coisa prática sobre isso acontecendo por aí para discutir. Ainda sim vou tentar ser mais direto e prático do que a maioria do conteúdo que estudei sobre isso.

Bit quântico - o que são os qubits?

Vamos começar do começo. Na computação clássica um bit só pode estar em um único estado, 1 ou 0. Ligado ou desligado. Acesso ou apagado. Com energia ou sem energia. Na computação quântica, um qubit, ou bit quântico, é a unidade básica de informação quântica, análogo ao bit na computação clássica. No entanto, enquanto um bit clássico pode estar em um de dois estados, um qubit pode existir em uma sobreposição desses estados.

Isso significa que o estado de um qubit é uma combinação dos dois estados. É como se ele estivesse um pouco no estado 1 e um pouco no estado 0 ao mesmo tempo. Esse "um pouco em cada estado" é uma probabilidade α de estar no estado 0 e β de estar no estado 1. Por fim, essa combinação de 0 e 1 gera um estado do qubit definido como ∣ψ⟩.

Além disso, a soma do quadrado das probabilidades é 1. Se α for 0, então o estado será 1 e se β for 0, o estado será 0.

Até aqui as coisas ainda estão simples. Entretanto, alfa (α) e beta (β) são números complexos na representação de estados quânticos de qubits devido a várias razões fundamentais inerentes à mecânica quântica e à natureza dos sistemas quânticos. Não vou entrar nesses detalhes, então você vai precisar só aceitar isso por enquanto.

Um número complexo é geralmente expresso na forma (a + bi), onde (a) é a parte real, (b) é a parte imaginária, e (i) é a unidade imaginária com a propriedade de que (i*i = -1).

Vamos a um exemplo prático e supor dois valores de alfa e beta.

Nesse exemplo, α e β tem magnitudes iguais. Isso significa que o estado ∣ψ⟩ representado por estes α e β é uma superposição dos estados ∣0⟩ e ∣1⟩ com igual probabilidade (devido às magnitudes iguais de α e β). Este estado significa que, ao medir este qubit, há uma probabilidade igual (50%) de obter ∣0⟩ ou ∣1⟩ devido às magnitudes iguais de α e β.

O papel da fase

Embora esses α e β tenham magnitudes iguais, eles não são iguais no componente complexo. Isso significa que existe uma diferença na fase desses números. Calculando as fases de α e β vamos encontrar:

Essa diferença de fase de 120 graus entre os dois estados base não afeta diretamente as probabilidades de medição em um único qubit isolado. Ou seja, se formos medir somente um qubit, a probabilidade será 50% para o estado 1 e 50% para o estado 0, pois somente a magnitude importará.

Por outro lado, quando consideramos interações entre qubits, como em sistemas de múltiplos qubits, as fases desempenham um papel fundamental. A interferência quântica é um fenômeno crucial que permite que os qubits interajam de maneira não trivial, especialmente em sistemas com múltiplos qubits. A fase relativa entre os estados de qubits individuais pode levar à interferência construtiva ou destrutiva, afetando o resultado de medições e operações.

Por exemplo, se aplicarmos uma operação entre dois qubits e depois medimos, podemos encontrar que a interferência entre os estados afeta a probabilidade de certos resultados, podendo aumentar ou reduzir a probabilidade dependendo do valor da fase.

Coordenadas Polares e a Esfera de Bloch

Os coeficientes α e β definem a amplitude de probabilidade e a fase do estado quântico. Eles podem ser expressos em termos das coordenadas polares θ e ϕ da seguinte maneira:

• θ varia de 0 a π e determina a proporção das amplitudes de probabilidade dos estados ∣0⟩ e ∣1⟩.
• ϕ varia de 0 a 2π e representa a diferença de fase entre os estados ∣0⟩ e ∣1⟩.

Podemos representar o estado de um qubit na esfera de Bloch, usando coordenadas polares. Essa é uma maneira de visualizar o estado quântico de forma geométrica. Para um estado quântico genérico ∣ψ⟩=α∣0⟩+β∣1⟩, onde α e β são números complexos, a representação na esfera de Bloch é dada pelas coordenadas polares (θ,ϕ).

Na esfera de Bloch:

• O eixo vertical (Z) representa os estados puros ∣0⟩ (no polo norte) e ∣1⟩ (no polo sul).
• A latitude, determinada pelo ângulo θ, indica a superposição dos estados ∣0⟩ e ∣1⟩.
• A longitude, determinada pelo ângulo ϕ, representa a diferença de fase entre os estados.

No cenário mais simples em que α=0, sabemos que o estado ∣ψ⟩ do qubit será ∣1⟩. Em coordenadas polares, ϕ será 0 e θ será π. A esfera de Bloch ficará assim.

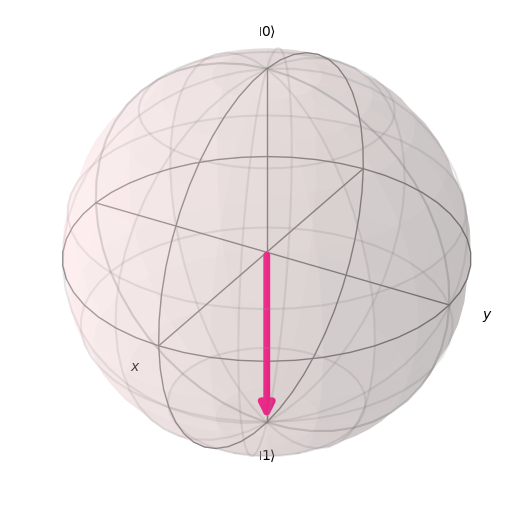
Vamos para o outro cenário discutido anteriormente em que:

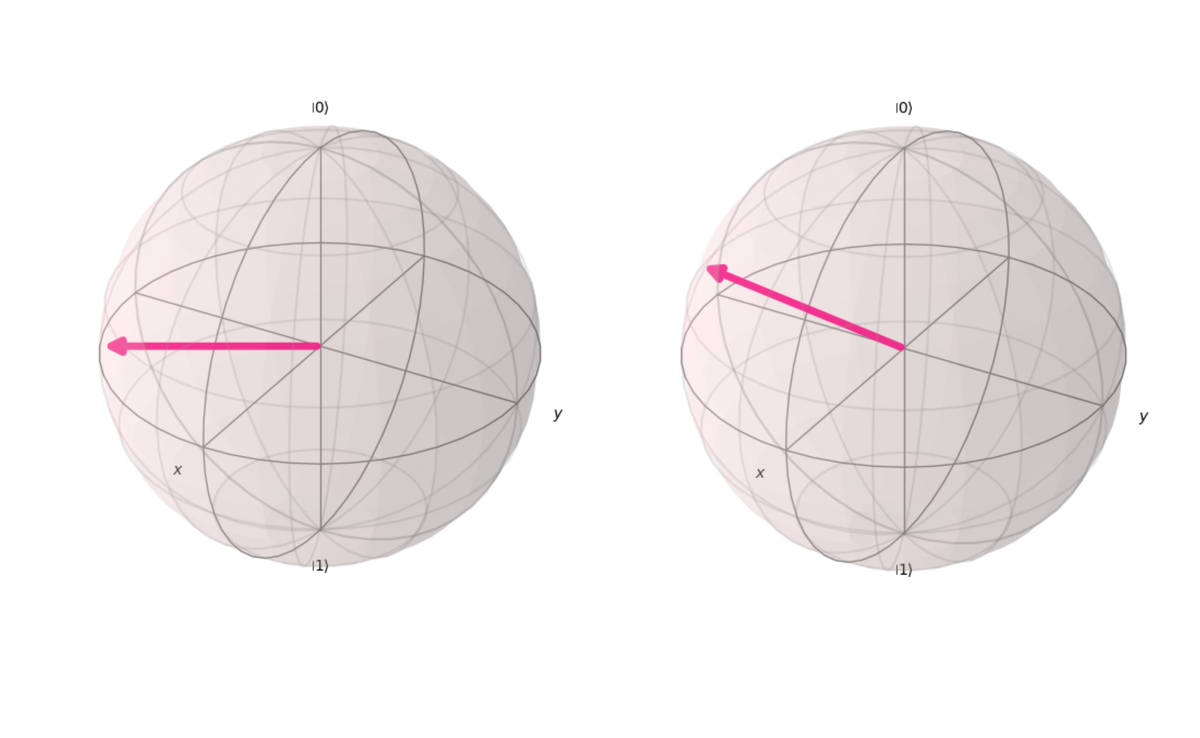
Nesse cenário, θ será π, o que coloca o ponto na Esfera de Bloch no equador, não no polo. O ângulo ϕ deve refletir a diferença de fase entre α e β e nesse caso será 5π/3.

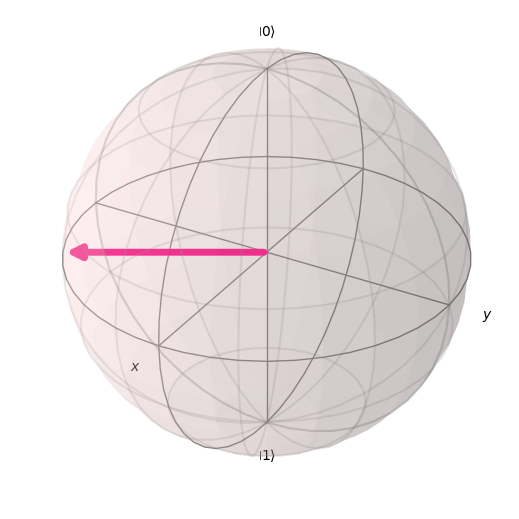
Para ajudar a visualizar melhor essas rotações, é assim que irá ocorrer o giro em torno do eixo x a medida que variamos o valor de θ.

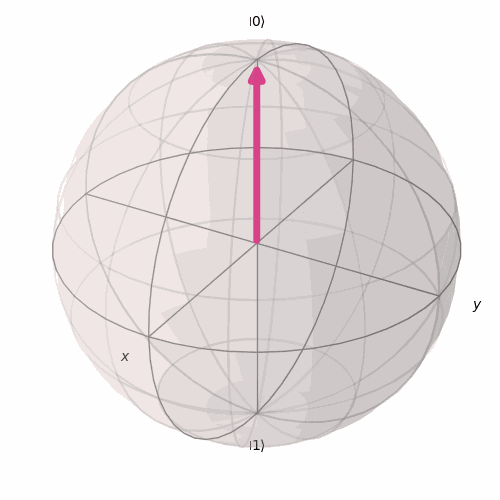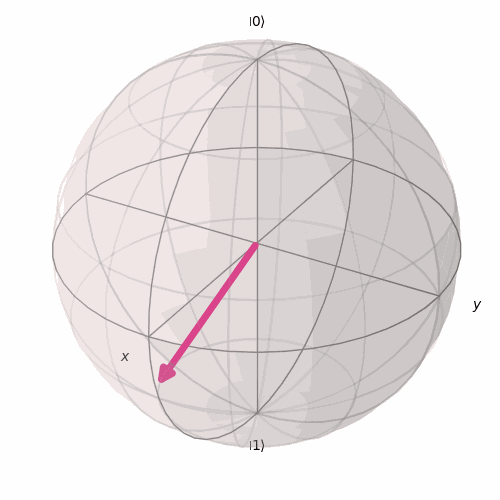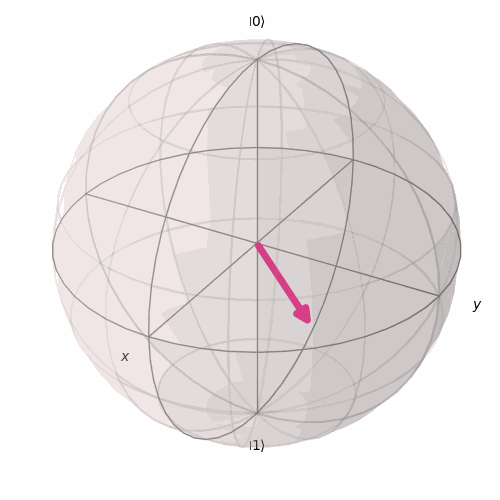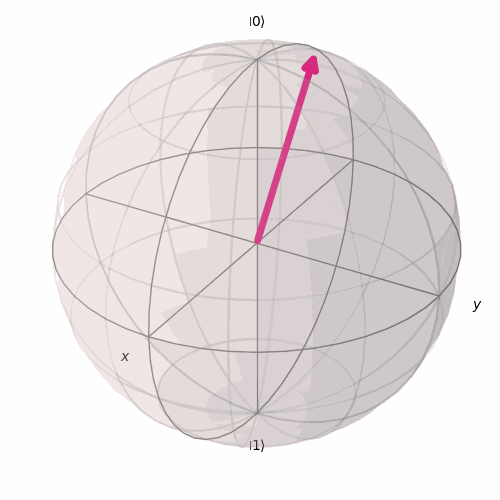
E é assim que irá girar em torno do eixo y a medida que variamos ϕ para um θ fixo.

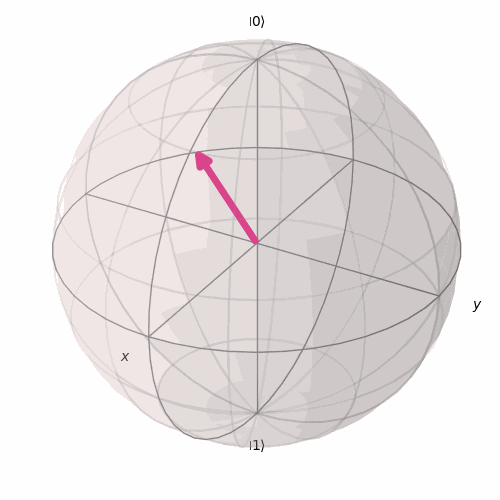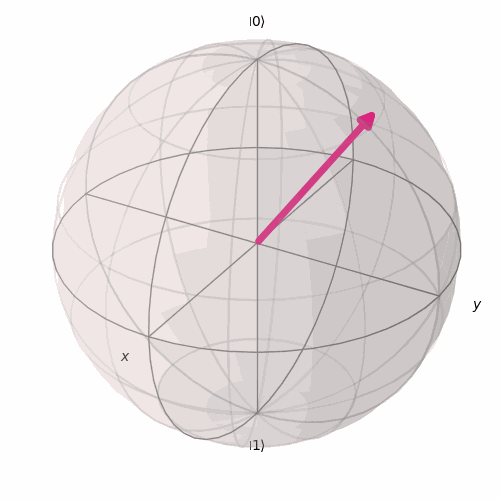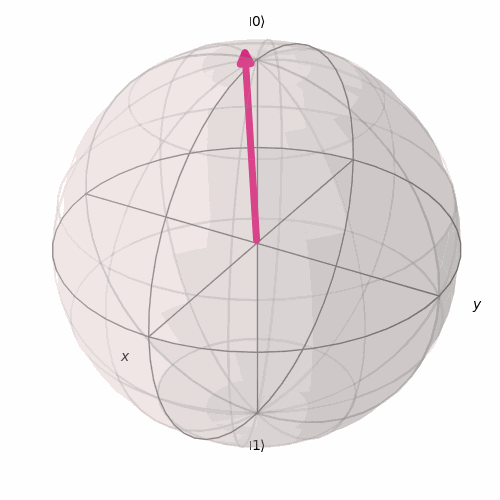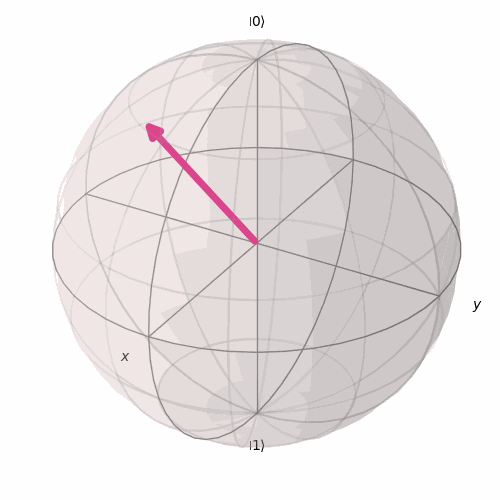
Conclusão

Meu objetivo com esse post era somente explorar o que são os qubits e como ter uma noção de como eles se comportam. Isso é o básico do básico, mas é a base para começar a entender como operações são realizadas na computação quântica.

Quero em aprofundar mais nesse tema por curiosidade, então provavelmente trarei outros artigos sobre o assunto a medida que for explorando esses conceitos.

Nos vemos na próxima 😃