Computação Quântica: Buscando um Elemento em uma Lista

A computação quântica continua atraindo muita minha atenção por seu potencial em resolver problemas que são desafiadores para a computação clássica. Comecei a colocar a bola no chão e tentar explorar de forma mais prática como seria o mundo em que criamos algoritmos voltados para computadores quânticos. O Algoritmo de Grover é um exemplo interessante pois resolve um problema bastante comum na computação clássica: busca de um elemento em uma lista desordenada.

Neste artigo vou mergulhar mais fundo no Algoritmo de Grover, explorando como ele funciona, por que ele é eficiente e, o mais importante, como ele pode ser usado para resolver um problema real: encontrar o primeiro número par em uma lista de números.

O Problema Clássico de Busca

Imagine que você tem a seguinte lista de números: [1, 3, 5, 7, 8, 9, 11, 13], e seu objetivo é encontrar o primeiro número par. Em um computador clássico, você percorreria a lista verificando cada elemento até encontrar o número desejado. Para essa lista específica, o primeiro número par é 8, e a busca clássica exigiria percorrer os primeiros quatro elementos antes de encontrar 8. Se a lista fosse muito maior, o tempo de busca poderia aumentar significativamente.

O Algoritmo de Grover oferece uma maneira de realizar essa busca de forma muito mais eficiente, especialmente quando a lista é grande.

Introduzindo o Algoritmo de Grover

O Algoritmo de Grover é um algoritmo quântico que resolve o problema da busca em listas desordenadas com uma complexidade de %%\mathcal{O}(\sqrt{N})%% , onde N é o número de elementos na lista. Isso significa que, para uma lista de N elementos, Grover pode encontrar a solução com aproximadamente %%\sqrt{N} %% operações, uma melhoria significativa em relação ao %%\mathcal{O}(N)%% das buscas clássicas.

Como o Algoritmo de Grover Funciona

O Algoritmo de Grover é composto por quatro etapas principais:

1. Superposição Inicial: Colocar todos os possíveis estados quânticos em superposição.

2. Oracle: Marcar o estado que corresponde à solução correta invertendo sua fase.

3. Amplificação da Amplitude (Inversão sobre a Média): Aumentar a probabilidade de medir o estado correto.

4. Medição: Medir os qubits para identificar o estado que foi amplificado.

Vamos detalhar cada uma dessas etapas e implementar um exemplo prático em Python usando o Qiskit.

1 - Superposição: Explorando Todos os Estados Simultaneamente

A computação quântica permite que todos os estados possíveis de um sistema sejam explorados simultaneamente, graças à superposição. No Algoritmo de Grover, começamos aplicando portas Hadamard a todos os qubits, o que coloca o sistema em uma superposição uniforme de todos os estados possíveis.

Por exemplo, se estivermos usando 3 qubits para representar nossa lista, após aplicar a porta Hadamard, todos os %%2^3 = 8%% estados possíveis estarão em superposição, com cada estado representando um número da lista.

from qiskit import QuantumCircuit

n_qubits = 4  # Vamos usar 4 qubits para representar nossa lista
qc = QuantumCircuit(n_qubits)

# Passo 1: Superposição inicial usando portas Hadamard
qc.h(range(n_qubits))
print(qc.draw())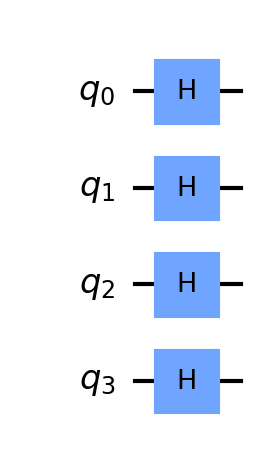

Podemos plotar as probabilidades e observar que, inicialmente, todos os estados tem a mesma probabilidade. Isso indica que todos os estados coexistem com a mesma probabilidade nesse instante.

from qiskit import QuantumCircuit, Aer, execute
from qiskit.visualization import plot_histogram

qc.measure_all()

# Executando o circuito
simulator = Aer.get_backend('aer_simulator')
result = execute(qc, backend=simulator, shots=1000).result()

# Exibindo os resultados
counts = result.get_counts(qc)
print("\nResultados da simulação:", counts)

# Plotando o histograma das probabilidades
plot_histogram(counts)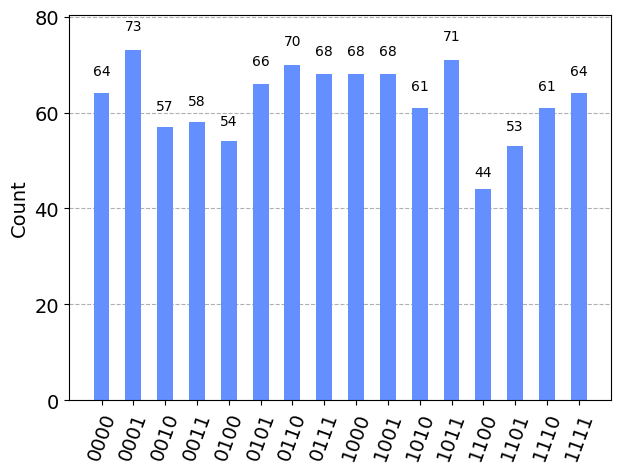

2 - Oracle: A Marcação do Estado Correto

O Oracle é a parte do Algoritmo de Grover que identifica o estado correto – o estado que estamos procurando. Ele faz isso invertendo a fase desse estado, ou seja, multiplicando a amplitude do estado por -1.

O ponto chave é que o Algoritmo de Grover pressupõe que temos uma forma de “testar” se um determinado estado é a solução que estamos procurando, mesmo sem saber de antemão qual é a solução.

2.1 - Função %%f(x)%% e Oracle

O Oracle no Algoritmo de Grover é uma função que podemos aplicar a qualquer estado %%x%% para verificar se ele é a solução que estamos procurando. Em termos simples, o Oracle é uma função %%f(x)%% que retorna 1 se %%x%% for a solução e 0 caso contrário.

A “marca” que o Oracle aplica ao estado quântico não nos diz diretamente qual é o estado correto; em vez disso, ele inverte a fase do estado quântico associado à solução.

2.2 - Estado Inicial e Superposição

No início, todos os estados possíveis estão em superposição. Isso significa que o sistema “explora” todos os estados simultaneamente. Quando o Oracle é aplicado, ele não precisa “saber” qual é o estado correto; ele simplesmente verifica cada estado em paralelo, marcando (invertendo a fase) do estado que satisfaz a condição %%f(x) = 1%%.

Suponha que queremos encontrar o número par em uma lista. O Oracle, então, é uma função que verifica se um número é par.

Quando aplicamos o Oracle em todos os estados (que representam os números na lista), ele marca o estado que representa o número par. A inversão de fase é uma operação que não nos revela diretamente o número, mas altera a forma como o estado interfere no processo subsequente.

2.3 - Mas por que inverter a fase?

Essa inversão é crucial porque prepara o terreno para a próxima etapa, onde a amplificação da amplitude faz com que o estado correto se destaque.

Situação Inicial:

1. Temos 4 estados: %%|00\rangle%%, %%|01\rangle%%, %%|10\rangle%%, %%|11\rangle%%.
2. Após a aplicação da porta Hadamard, todos os estados têm a mesma amplitude %%\alpha = \frac{1}{2}%%.

Após o Oracle:

1. Suponha que o estado %%|11\rangle%% é o estado marcado. Após o Oracle, sua amplitude se torna %%-\frac{1}{2}%%.

No exemplo de busca pelo primeiro número par, o Oracle seria programado para identificar estados que representam números pares e inverter suas fases.

def oracle(qc, n_qubits, binary_rep):
    for state in binary_rep:
        number = int(state, 2)
        if number % 2 == 0:  # Se o número for par
            for qubit in range(n_qubits):
                print(qubit, state[qubit])
                if state[qubit] == '0':
                    qc.x(n_qubits-qubit-1)
            
            qc.h(n_qubits-1)
            qc.mct(list(range(n_qubits-1)), n_qubits-1)
            qc.h(n_qubits-1)
            
            for qubit in range(n_qubits):
                print(qubit, state[qubit], n_qubits-qubit-1)
                if state[qubit] == '0':
                    qc.x(n_qubits-qubit-1)

2.4 - Explicando o algoritmo

1. Iteramos sobre os estados possíveis na lista binary_rep
2. Verificamos se o número correspondente ao estado é par
3. Marcamos esse estado aplicando uma série de portas quânticas. Primeiro a porta X nos qubits que têm '0' no estado binário.
   1. Por que a Porta X é Aplicada Apenas nos Qubits que Têm %%\vert 0 \rangle%%?
   2. A porta Toffoli, que é uma versão controlada de uma porta NOT, exige que todos os seus qubits de controle estejam no estado %%\vert 1 \rangle%% para executar a operação de inversão (NOT) no qubit alvo. Se um qubit de controle estiver no estado %%\vert 0 \rangle%%, a porta Toffoli não realizará a inversão do qubit alvo.
4. A porta Hadamard é então aplicada ao último qubit para preparar o estado para a porta Toffoli que é usada para inverter a fase do estado.
   1. Isso é necessário porque a porta Hadamard transforma o qubit de alvo de forma a criar uma superposição entre os estados %%\vert 0 \rangle%% e %%\vert 1 \rangle%%. Essa superposição permite que a porta Toffoli, que é controlada pelos qubits de controle, realize a inversão da fase de maneira condicional. Sem a porta Hadamard, o qubit de alvo estaria em um estado fixo (%%\vert 0 \rangle%% ou %%\vert 1 \rangle%%), e a porta Toffoli não poderia realizar a inversão de fase necessária no estado marcado pelo Oracle.
5. A porta Toffoli (mct: multiple controlled Toffoli) é aplicada, condicionada aos qubits de controle. Isso inverte o qubit de fase do estado marcado.
   1. Isso é necessário porque a porta Toffoli permite que a inversão de fase ocorra apenas quando todos os qubits de controle estão no estado %%\vert 1 \rangle%%. No contexto do Algoritmo de Grover, queremos inverter a fase de um estado específico (o estado marcado pelo Oracle). A porta Toffoli (ou mct) realiza essa inversão de fase de maneira condicional, garantindo que o qubit de fase seja invertido apenas para o estado que corresponde à solução correta. Sem essa condição imposta pelos qubits de controle, a inversão de fase não seria seletiva, e todos os estados poderiam ser afetados, o que comprometeria a eficácia do algoritmo.
6. A porta Hadamard é novamente aplicada ao último qubit para reverter a preparação.
7. Finalmente, revertendo as portas X aplicadas anteriormente para retornar os qubits ao estado original.

2.5 - Exemplo Visual - Circuito Quântico Simplificado:

Vamos considerar um exemplo com 3 qubits onde queremos marcar o estado %%\vert 010 \rangle%% (equivalente ao número 2).

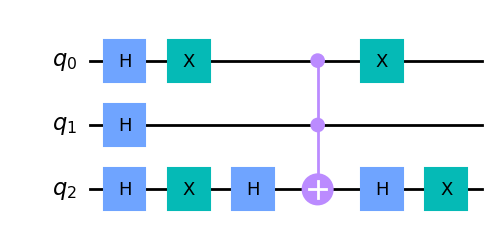
1. Portas Hadamard (H) são aplicadas inicialmente para colocar todos os qubits em superposição.
2. Portas X são aplicadas ao primeiro e terceiro qubits (representando %%\vert 0 \rangle%% bits) para que a porta Toffoli possa operar corretamente.
3. Porta Toffoli (•) conectada ao (⊕) no terceiro qubit, inverte a fase do terceiro qubit (quando necessário).
4. Portas X são aplicadas novamente para reverter as mudanças iniciais nos qubits de controle.

3 - Amplificação da Amplitude: O Segredo da Eficiência

Após a fase do estado correto ser invertida pelo Oracle, entra em cena a amplificação da amplitude. Esse processo, conhecido como inversão sobre a média, aumenta a amplitude do estado marcado, enquanto reduz a amplitude dos outros estados. Mas como isso funciona?

A amplificação da amplitude pode ser visualizada como uma reflexão em torno da média das amplitudes. Após a inversão de fase, o estado marcado tem uma amplitude negativa, enquanto os outros estados mantêm suas amplitudes positivas. A inversão sobre a média reflete todos esses estados em torno da média das amplitudes, resultando em um aumento da amplitude do estado marcado.

Aqui é onde o "ganhar peso" acontece, e envolve dois passos principais:

a. Cálculo da Média das Amplitudes

• Antes de aplicar a inversão sobre a média, todos os estados têm a mesma amplitude (exceto o estado marcado, que foi invertido).
• Suponha que temos %%M%% estados com amplitudes %%\alpha_1, \alpha_2, \ldots, \alpha_M%%, com o estado marcado tendo %%-\alpha_m%% após o Oracle.
• A média das amplitudes %%\bar{\alpha}%% é calculada considerando todos os estados.

b. Reflexão das Amplitudes em Torno da Média

• Agora, todos os estados são "refletidos" ao redor da média %%\bar{\alpha}%%.
  • Estados não marcados: Se um estado tinha amplitude %%\alpha_i%% maior que a média %%\bar{\alpha}%%, ele será refletido para uma amplitude menor (e vice-versa).
  • Estado marcado: Como o estado marcado começou com uma amplitude %%-\alpha_m%% (depois da inversão de fase), que é significativamente diferente da média, essa reflexão o move para uma amplitude ainda maior, resultando em um aumento substancial de sua probabilidade.

3.1 - Visualização Matemática da Inversão sobre a Média

Vamos ver isso com um exemplo simplificado:

Situação Inicial:

• Temos 4 estados: %%\vert 00 \rangle, \vert 01 \rangle, \vert 10 \rangle, \vert 11 \rangle%%.
• Após a aplicação da porta Hadamard, todos os estados têm a mesma amplitude %%\alpha = \frac{1}{2}%%.

Após o Oracle:

• Suponha que o estado %%\vert 11 \rangle%% é o estado marcado. Após o Oracle, sua amplitude se torna %%-\frac{1}{2}%%.

Média das Amplitudes:

• Antes da inversão sobre a média, as amplitudes são %%\frac{1}{2}, \frac{1}{2}, \frac{1}{2}, -\frac{1}{2}%%.
• A média %%\bar{\alpha}%% dessas amplitudes é %%\frac{1}{4}%%.

Inversão sobre a Média:

• Para cada amplitude %%\alpha_i%%, a nova amplitude %%\alpha_i'%% após a inversão sobre a média é dada por: αi′=2αˉ−αi\alpha_i' = 2\bar{\alpha} - \alpha_iαi′​=2αˉ−αi​
• Aplicando isso:
  • Estados não marcados: Se %%\alpha_i = \frac{1}{2}%%, a nova amplitude será %%\alpha_i' = 2(\frac{1}{4}) - \frac{1}{2} = 0%%.
  • Estado marcado %%\vert 11 \rangle%%: A nova amplitude será %%\alpha_{\vert 11 \rangle}' = 2(\frac{1}{4}) - (-\frac{1}{2}) = 1%%.

Resultado Final:

• Estado marcado: Sua amplitude passou de %%-\frac{1}{2}%% para %%1%%, o que significa que sua probabilidade de ser medido aumentou significativamente.
• Estados não marcados: Suas amplitudes foram reduzidas, diminuindo a probabilidade de serem medidos.

3.2 - Por que isso funciona?

• Interferência Construtiva: A inversão sobre a média cria interferência construtiva para o estado marcado, aumentando sua amplitude.
• Interferência Destrutiva: Ao mesmo tempo, ela reduz a amplitude dos estados não marcados, criando interferência destrutiva.

3.3 - Iterações Adicionais

• Em um algoritmo completo de Grover, esse processo é repetido várias vezes (em torno de %%\sqrt{N}%% vezes para %%N%% estados) para aumentar ainda mais a probabilidade do estado marcado, até que ele seja quase certamente o estado medido ao final.

3.4 - Exemplo Visual do Circuito

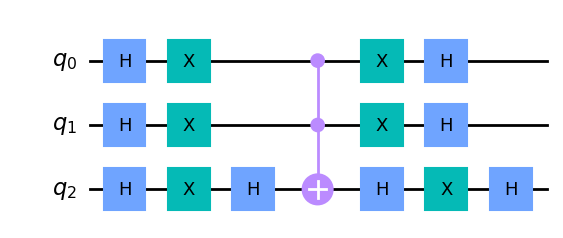
1. Portas Hadamard (H):
   • Aplicadas inicialmente a todos os 3 qubits, essas portas criam uma superposição.
2. Portas X (NOT):
   • Aplicadas a todos os qubits, preparando-os para a operação de Toffoli.
3. Porta Hadamard no Último Qubit:
   • Aplicada ao qubit 2 para preparar a operação da porta Toffoli.
4. Porta Toffoli (CCX):
   • Controlada pelos qubits 0 e 1, com o qubit 2 como alvo. Esta operação inverte o estado do qubit 2 condicionalmente.
5. Reversão das Operações:
   • As portas Hadamard e X são revertidas para finalizar a amplificação da amplitude.

4 - Medição: A Conclusão da Busca

Após aplicar a superposição, o Oracle, e a amplificação da amplitude, os qubits estão prontos para serem medidos. A medição colapsa o estado quântico em um dos estados possíveis, e o estado que foi amplificado pelo Algoritmo de Grover terá a maior probabilidade de ser medido.

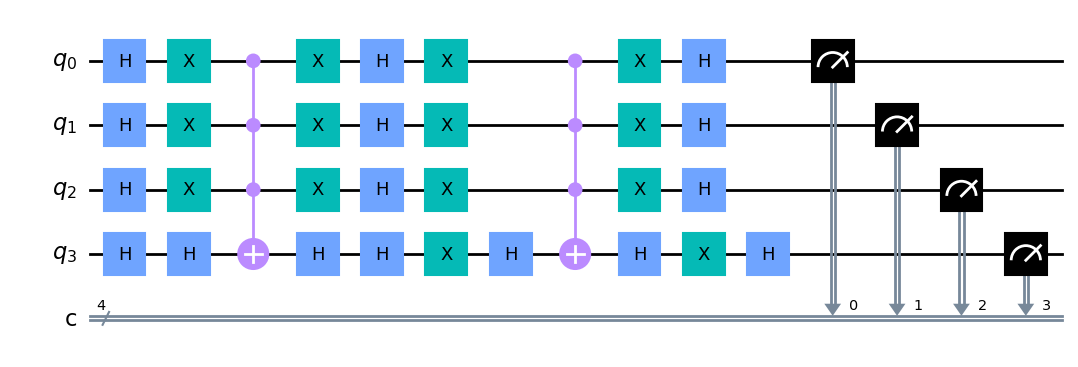
O circuito completo está apresentado abaixo, onde a última etapa é a medição.

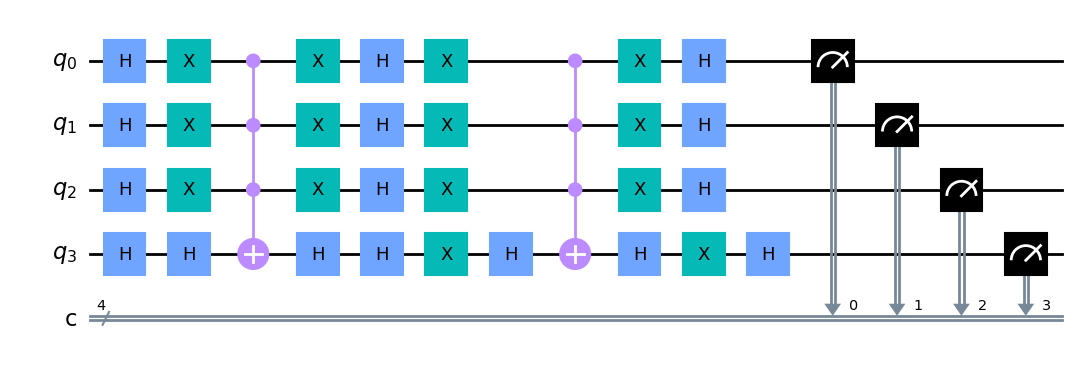
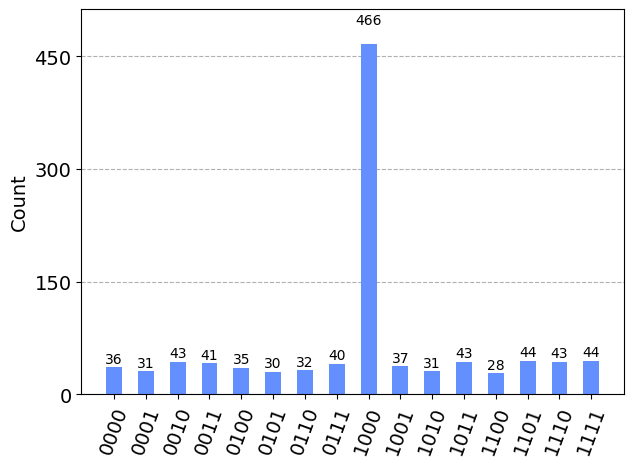
O estado correspondente ao número 8 (em binário 1000) terá uma contagem significativamente maior no histograma resultante. Isso mostra que o Algoritmo de Grover identificou corretamente o número 8 como o primeiro número par na lista, com muito menos operações do que seria necessário em uma busca clássica.

Conclusão

O Algoritmo de Grover é uma ferramenta poderosa que mostra como a computação quântica pode acelerar a resolução de problemas complexos. No exemplo da busca pelo primeiro número par em uma lista, vimos como o Algoritmo de Grover pode encontrar a solução em muito menos passos do que um algoritmo clássico.

Enquanto a computação quântica ainda está em seus estágios iniciais, entender algoritmos como o de Grover ajuda a ter uma visão mais clara de qual caminho podemos seguir.