Como transformar lucro em prejuízo com uma análise míope: um exercício de inferência causal e segmentação

Inferência causal é um dos pilares mais desafiadores e fascinantes da análise de dados: diferenciar correlação de causalidade e entender como cada decisão afeta diretamente os resultados. Em contextos onde existe uma segmentação de público, como em campanhas de marketing, saber como alocar cada usuário no grupo certo pode ser a diferença entre lucro e prejuízo.
Para ilustrar esse conceito, quero explorar um case prático de marketing, onde diferentes campanhas apresentam custos e taxas de conversão variados.
Introdução ao Cenário
Imagine que uma empresa tenha realizado quatro campanhas de marketing distintas, cada uma com um custo e uma taxa de conversão diferentes. A campanha A1 custa R$150 por usuário, A2 custa R$120, B1 custa R$50 e B2 custa R$80. Cada usuário convertido gera uma receita de R$250. Agora, para saber qual dessas campanhas traz o melhor retorno financeiro, não basta olhar apenas para as taxas de conversão; é preciso entender o impacto que cada campanha causa em diferentes segmentos de usuários.
| Campanha | Custo por Usuário |
|---|---|
| A1 | R$ 150 |
| A2 | R$ 120 |
| B1 | R$ 50 |
| B2 | R$ 80 |
Imagine que você recebeu uma base de dados com as seguintes colunas: ID, Score, Campanha e Conversão. Essa base contém diversos usuários que foram atingidos com uma campanha específica de marketing e podem ou não terem se convertido em uma venda. O Score é utilizado de forma a segmentar seus usuários, de forma que usuários com um score maior são mais propensos a se converterem. Esse cenário deve soar familiar se você já trabalhou com testes A/B ou com qualquer tipo de política construída a partir de um modelo. Você pode baixar o CSV com esses dados abaixo caso queira acompanhar o raciocínio de forma prática.
Explorando as Taxas de Conversão por Campanha
Você, como um bom e ansioso curioso, vai querer saber diretamente qual a taxa de conversão de cada campanha nessa base.
import pandas as pd
df = pd.read_csv("df_selected.csv")
df.groupby("campaign")[['real_conversion']].agg(['mean', 'count'])| Campaign | Real Conversion (%) | Count |
|---|---|---|
| A1 | 89% | 1086 |
| A2 | 53% | 1079 |
| B1 | 38% | 1654 |
| B2 | 38% | 1699 |
E pronto, análise finalizada. Sua conclusão seria que a campanha A1 é extraordinária e deveria ser usadas em todo e qualquer cenário? Será realmente verdade? Let's look deeper!
Avaliando o Retorno sobre Investimento (ROI)
Você conhece o custo de cada campanha e o retorno de uma conversão. Se você inserir esses dados em sua análise, é capaz de calcular o retorno sobre o investimento de cada cenário. Essa é uma métrica mais interessante, pois mesmo que as campanhas A1 e B1 tenham conversões bem diferentes, elas também possuem custos diferentes. A1 é muito mais cara, mas também trás uma conversão muito melhor.
import numpy as np
campaign_costs = {
'A1': 150,
'A2': 120,
'B1': 50,
'B2': 80
}
df['campaign_cost'] = df['campaign'].map(campaign_costs)
df['revenue'] = df['real_conversion'] * 250
df['profit'] = df['revenue'] - df['campaign_cost']
result = df.groupby("campaign")[['profit']].agg(['sum', 'count'])
result['roas'] = result[('profit', 'sum')] / result[('profit', 'count')]
result
| Campaign | Profit (R$) | Count | ROAS (R$) |
|---|---|---|---|
| A1 | 79,100.00 | 1086 | 72.84 |
| A2 | 12,270.00 | 1079 | 11.37 |
| B1 | 74,800.00 | 1654 | 45.22 |
| B2 | 25,580.00 | 1699 | 15.06 |
Mas qual o lucro final da operação? Se somarmos a coluna de Profit, obteremos R$ 191.750,00 reais e 5.518 usuários. Entretanto, se a campanha A1 tem um ROAS de R$ 72,84/usuário, tínhamos potencial para obter um lucro de R$ 401.875,94 se tivéssemos enviado somente a campanha A1? Será que a relação é tão direta quanto uma simples regra de 3? Poderíamos ter lucrado o dobro somente com uma troca de campanha?
Segmentação por Score e Impacto nas Campanhas
Note que existem outros dados disponíveis em sua base. Existe um score que distingue um usuário de outro. Observe a distribuição dos scores dessa base.
import seaborn as sns
sns.displot(df, x="score")
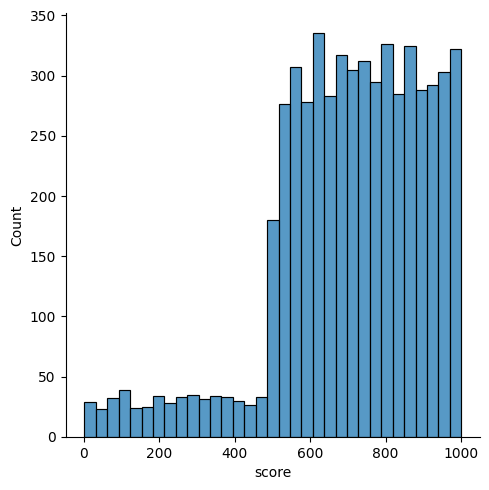
Existem pouquíssimos usuários com score < 500 em comparação aos usuários com score > 500. Isso significa que, ou existem poucos usuários com score < 500, ou existe uma segmentação que descarta esses usuários. Se usuários com maior score são mais propensos a converterem, então faz sentido não atender usuários com score muito baixo. Provavelmente eles não trariam o retorno desejado.
Perceba como o score mede de forma direta a probabilidade de conversão de um usuário. Isso significa que podemos usar o score para direcionar nossas ações. Mas também significa que precisamos usar ele em nossas análises.
from matplotlib import pyplot as plt
df['score_band'] = pd.cut(df['score'], bins=range(0, 1001, 100), labels=[f'{i}-{i+99}' for i in range(0, 1000, 100)])
sns.barplot(x="score_band", y="real_conversion", data=df)
plt.xticks(rotation=45)
plt.show()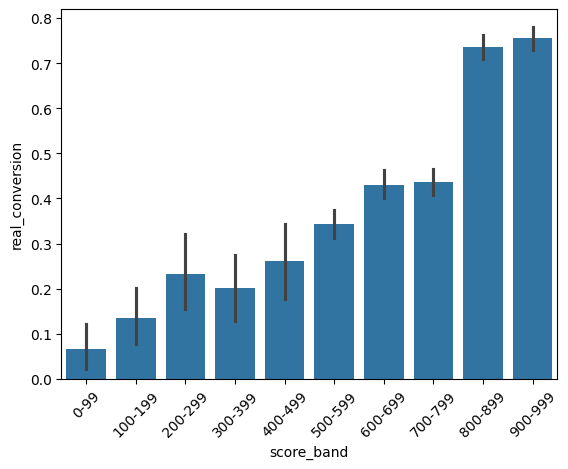
Observe o volume por banda e por campanha. Praticamente não temos sample das campanhas A1 e A2 para os scores < 500. Para as campanhas B1 e B2 temos um pouco mais de volume, mas ainda é pouco.
| Score Band | A1 | A2 | B1 | B2 |
|---|---|---|---|---|
| 0-99 | 5 | 4 | 42 | 39 |
| 100-199 | 6 | 1 | 51 | 46 |
| 200-299 | 7 | 7 | 41 | 48 |
| 300-399 | 5 | 9 | 45 | 50 |
| 400-499 | 5 | 3 | 41 | 47 |
| 500-599 | 50 | 50 | 403 | 472 |
| 600-699 | 59 | 50 | 467 | 450 |
| 700-799 | 44 | 53 | 457 | 439 |
| 800-899 | 481 | 433 | 55 | 54 |
| 900-999 | 424 | 469 | 52 | 54 |
Isso significa que se olharmos a conversão segmentando a base de usuários por faixa de score, nossa conclusão seria extremamente errática pois temos pouquíssimo volume em diversas regiões. Ainda assim, a conversão da campanha A1 para score > 800 é extremamente boa.
| Score Band | A1 | A2 | B1 | B2 |
|---|---|---|---|---|
| 0-99 | 20% | 25% | 5% | 5% |
| 100-199 | 0% | 0% | 16% | 13% |
| 200-299 | 29% | 29% | 20% | 25% |
| 300-399 | 0% | 11% | 22% | 22% |
| 400-499 | 0% | 67% | 22% | 30% |
| 500-599 | 40% | 32% | 37% | 32% |
| 600-699 | 42% | 48% | 43% | 43% |
| 700-799 | 34% | 45% | 43% | 45% |
| 800-899 | 100% | 51% | 45% | 50% |
| 900-999 | 100% | 59% | 44% | 59% |
Note como existem alguns viéses aqui. Primeiramente, as campanhas A1 e A2 tem pouquíssimo volume para as bandas < 500. Isso significa que existe uma região dos dados que foi segmentada por algum motivo. Da mesma forma, existe muito mais volume de A1 e A2 para > 800. As campanhas B1 e B2 também tem diferenças de volume a depender do recorte de score, com as quebras também em 500 e 800. Ou seja, existem 3 regiões: 0 a 500, 500 a 800 e maior que 800.
Como tirar conclusões onde não existem dados? como confiar que essas conclusões estão corretas?
Construindo um Modelo de Regressão para Previsão de Conversão
Vamos usar uma regressão linear para analisar o impacto de diferentes campanhas na taxa de conversão. Usei smf.ols() para criar um modelo de regressão linear. O "ols" significa "Ordinary Least Squares" (Mínimos Quadrados Ordinários), que é uma técnica para estimar os parâmetros em um modelo linear. Nessa primeira versão, a única variável utilizada para estimar a conversão é a campanha.
import statsmodels.formula.api as smf
model = smf.ols(formula='real_conversion ~ C(campaign)', data=df).fit()
print(model.summary())
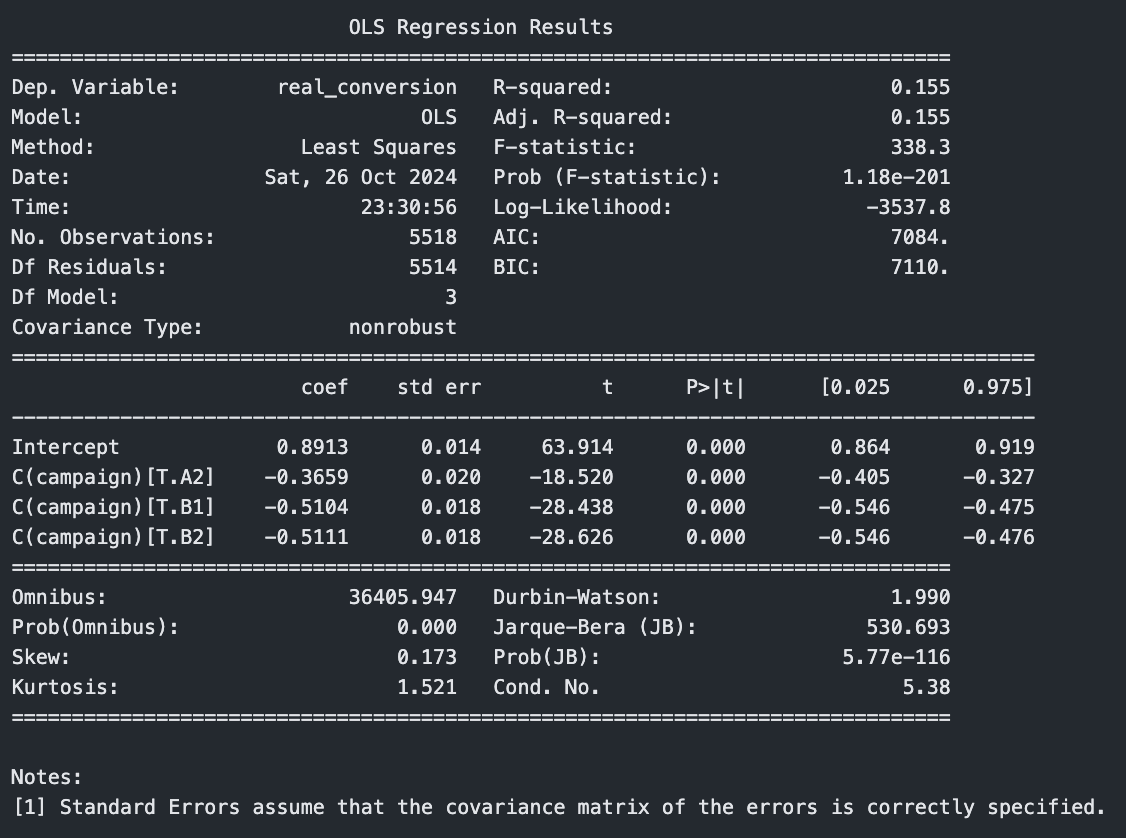
Observe os coeficientes. O intercepto é 0.89, o que significa 89% de chance de conversão para a campanha A1. O coeficiente para a campanha A2 é 0.36, o que significa que existe 36 pontos percentuais a menos do que no intercepto. Ou seja, 89 - 36 = 53% de chance de conversão para a campanha A2. O mesmo raciocínio vale para B1 e B2. Volte lá em cima desse artigo, na primeira tabela apresentada, de conversão por campanha. Perceba como o número é exatamente igual.
Se não existir nenhuma outra variável, essa é a conclusão. Entretanto, nós já observamos como existem quebras de comportamento a depender da região do score. Vamos incluir essa informação no dataframe e na ols.
df['score_region'] = np.where(df['score'] < 500, '< 500', np.where(df['score'] < 800, '500-800', '> 800'))
model = smf.ols(formula='real_conversion ~ C(campaign) + C(score_region)', data=df).fit()
print(model.summary())
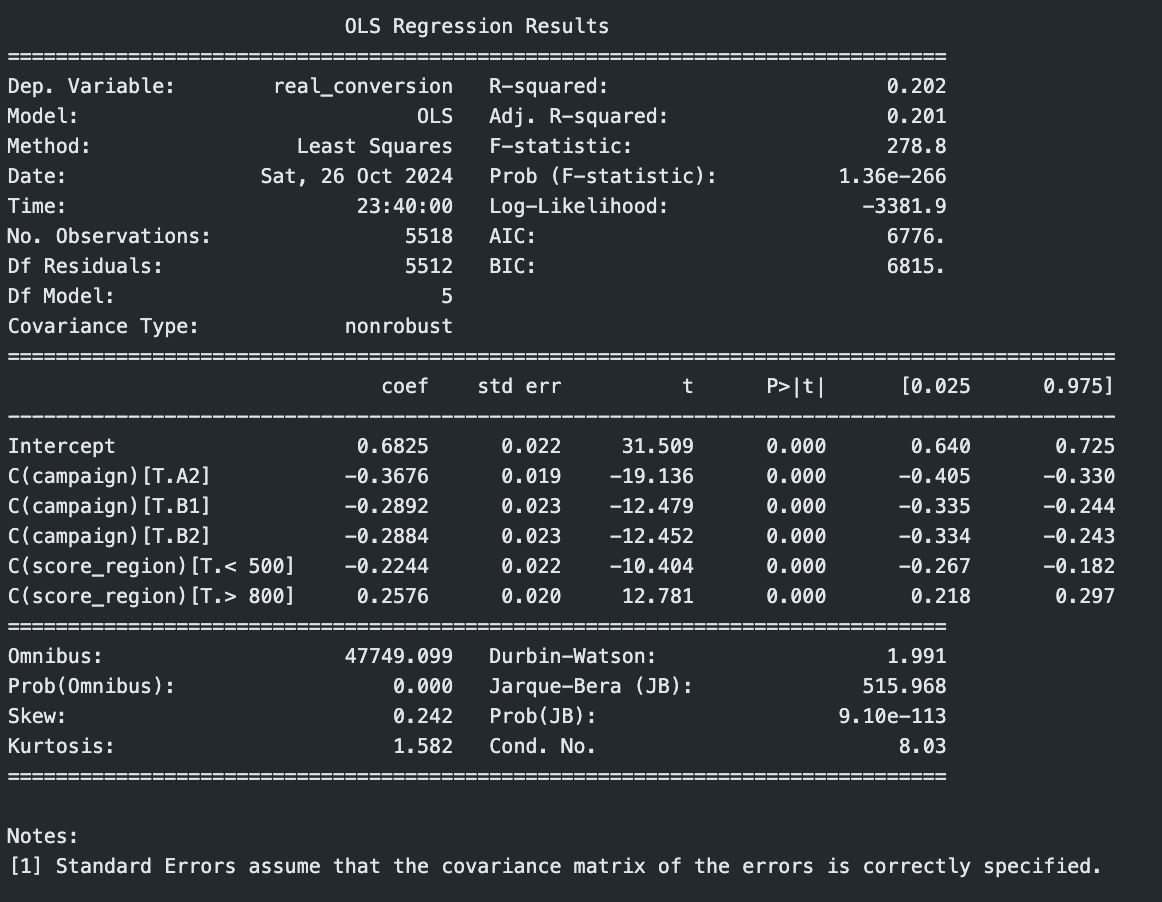
Observe novamente o intercepto. Deixou de ser 89% e passou a ser 68%. Como fica a conversão da campanha A1 agora? Note como não existe a região 500-800 nos coeficientes e nem a campanha A1. Isso significa que 68% é a probabilidade de um usuário com score 500-800 que recebeu a campanha A1 converter. Um usuário > 800 que recebeu a campanha A1 tem probabilidade 0.68 + 0.25 = 93%.
Você sempre pode calcular o score com essa regressão e os comparar com a conversão real. Observe que em alguns cenários os números são bastante parecidos, mas em outras é bem diferente. Observe também como os números são mais parecidos justamente nas regiões onde existem mais volume de dados.
df['predicted_conversion'] = model.predict(df)
df.groupby(["score_region", "campaign"])[['real_conversion', 'predicted_conversion']].mean()
| Score Region | Campaign | Real Conversion (%) | Predicted Conversion (%) |
|---|---|---|---|
| 500-800 | A1 | 39% | 68% |
| A2 | 42% | 31% | |
| B1 | 41% | 39% | |
| B2 | 40% | 39% | |
| < 500 | A1 | 11% | 46% |
| A2 | 25% | 9% | |
| B1 | 17% | 17% | |
| B2 | 20% | 17% | |
| > 800 | A1 | 100% | 94% |
| A2 | 55% | 57% | |
| B1 | 45% | 65% | |
| B2 | 55% | 65% |
O problema é que as duas variáveis que estamos usando interagem entre si. Nós já vimos como a campanha varia a depender da região. Isso significa que uma ação foi tomada considerando a região. As variáveis não são independentes.
Ajustando a regressão para interagir essas variáveis faz com que o resultado calculado pelo modelo seja exatamente igual ao resultado observado nos dados.
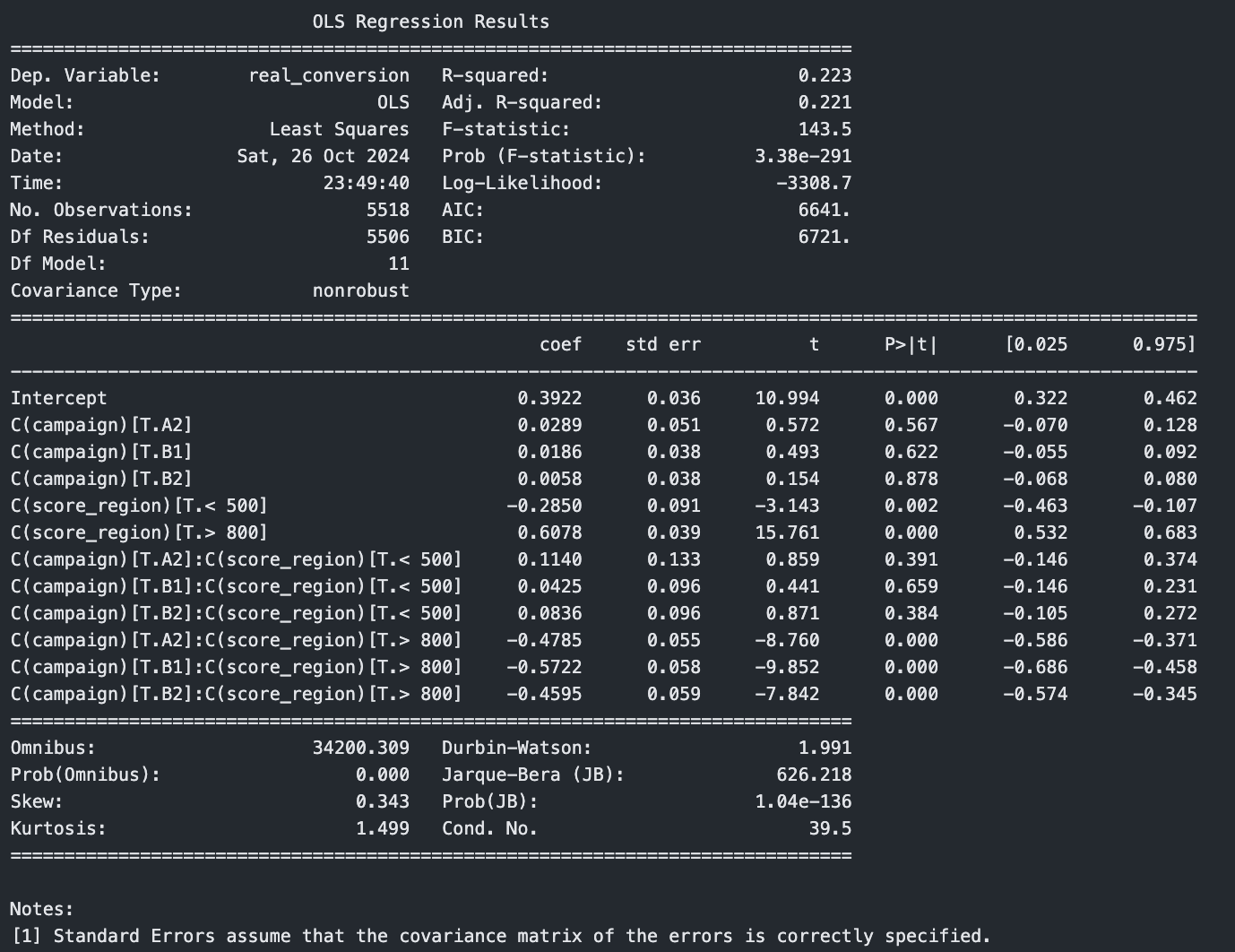
model = smf.ols(formula='real_conversion ~ C(campaign) * C(score_region)', data=df).fit()
print(model.summary())
df['predicted_conversion'] = model.predict(df)
df.groupby(["score_region", "campaign"])[['real_conversion', 'predicted_conversion']].mean()
| Score Region | Campaign | Real Conversion (%) | Predicted Conversion (%) |
|---|---|---|---|
| 500-800 | A1 | 39% | 39% |
| A2 | 42% | 42% | |
| B1 | 41% | 41% | |
| B2 | 40% | 40% | |
| < 500 | A1 | 11% | 11% |
| A2 | 25% | 25% | |
| B1 | 17% | 17% | |
| B2 | 20% | 20% | |
| > 800 | A1 | 100% | 100% |
| A2 | 55% | 55% | |
| B1 | 45% | 45% | |
| B2 | 55% | 55% |
Isso significa que temos um modelo que faz sentido com os dados que temos. Podemos estimar a probabilidade de conversão para cada usuário já considerando seu cenário: qual campanha ele recebeu? em qual região ele estava?
| Score Region | A1 | A2 | B1 | B2 |
|---|---|---|---|---|
| 500-800 | 39% | 42% | 41% | 40% |
| < 500 | 11% | 25% | 17% | 20% |
| > 800 | 100% | 55% | 45% | 55% |
Simulação e Otimização do Lucro
Agora você pode simular o que teria acontecido se todos os usuários tivessem recebido a campanha A1. Lembra que lá em cima ela tinha potencial para levar o lucro de ~200k para ~400k?
Observe como teria sido a conversão: 9% para usuários com score < 500 e 39% para usuários com score 500-800.
df_all_a1 = df.copy()
df_all_a1['campaign'] = 'A1'
df['predicted_conversion_a1'] = model.predict(df_all_a1)
result = df.groupby(["score_region"])[['predicted_conversion_a1']].agg(['mean', 'count'])
result
| Score Region | Predicted Conversion A1 (%) | Count |
|---|---|---|
| 500-800 | 39% | 2989 |
| < 500 | 9% | 501 |
| > 800 | 100% | 2028 |
E como teria sido a receita e lucro? Catastrófica. O lucro final teria sido R$ -19.525,00. Ou seja, ao invés de dobrar o lucro, você teria o tornado negativo.
result['revenue_a1'] = result[('predicted_conversion_a1', 'mean')] * 250
result['profit_a1'] = result[('revenue_a1')] - 150
result['sum_profit_a1'] = result[('profit_a1')] * result[('predicted_conversion_a1', 'count')]
result| Score Region | Predicted Conversion A1 (%) | Count | Revenue A1 | Profit A1 | Sum Profit A1 |
|---|---|---|---|---|---|
| 500-800 | 39% | 2989 | 97,12 | -52,88 | -158.044,24 |
| < 500 | 9% | 501 | 23,67 | -126,33 | -63.292,86 |
| > 800 | 100% | 2028 | 249,51 | 99,51 | 201.811,36 |
E como otimizar? você pode estimar o ROAS por região considerando a probabilidade individual de conversão. Dessa forma, cada usuário teria uma receita e um custo individual.
aux_conversion = df.groupby(["score_region", "campaign"])[['real_conversion']].mean().unstack()
aux_revenue = aux_conversion * 250
aux_profit = aux_revenue.copy()
for campaign, cost in campaign_costs.items():
aux_profit[('real_conversion', campaign)] = aux_profit[('real_conversion', campaign)] - cost
display(aux_profit)
| Score Region | A1 (R$) | A2 (R$) | B1 (R$) | B2 (R$) |
|---|---|---|---|---|
| 500-800 | -51,96 | -14,74 | 52,69 | 19,49 |
| < 500 | -123,21 | -57,50 | -7,95 | -30,87 |
| > 800 | 100,00 | 17,60 | 61,61 | 56,57 |
Note que para a região > 800, a campanha A1 trás um ROAS de R$ 100,00 e é a melhor opção. Para a região 500-800, a melhor opção é a campanha B1 que tem um ROAS de R$ 52,89. E, por fim, a região < 500 não trás lucro em nenhum cenário, mas perde menos com a campanha B1.
Isso significa que poderíamos ter enviado somente A1 para > 800 e somente B1 para todo o restante.
df_optimized = df.copy()
df_optimized['campaign'] = np.where(df_optimized['score'] > 800, 'A1', 'B1')
df_optimized['predicted_conversion_optimized'] = model.predict(df_optimized)
df_optimized['revenue_optimized'] = df_optimized['predicted_conversion_optimized'] * 250
df_optimized['profit_optimized'] = np.where(df_optimized['campaign'] == 'A1',
df_optimized['revenue_optimized'] - 150,
df_optimized['revenue_optimized'] - 50)
result_optimized = df_optimized.groupby('score_region').agg({
'predicted_conversion_optimized': ['mean', 'count'],
'profit_optimized': ['mean', 'sum']
})
result_optimized| Score Region | Predicted Conversion Optimized (%) | Count | Profit Optimized (Mean) | Profit Optimized (Sum) |
|---|---|---|---|---|
| 500-800 | 41% | 2989 | 52,30 | 156.338,18 |
| < 500 | 17% | 501 | -7,20 | -3.606,78 |
| > 800 | 100% | 2028 | 99,88 | 202.546,61 |
Nesse cenário, o lucro total teria sido R$ 355.278,01. Inicialmente, a alta taxa de conversão da campanha A1 sugeria ser a melhor opção; no entanto, ao considerar os custos e a distribuição de scores, descobrimos que aplicação universal da campanha A1 seria financeiramente catastrófica.
Simulando a utilização das campanhas A1 e B1 nas faixas de score >800 e <800, respectivamente, obteríamos um lucro otimizado de R$ 355.278,01, muito superior ao cenário inicial e muito mais seguro financeiramente do que simplesmente aplicar a campanha A1 que possui um custo muito mais alto.
Expansão da Cobertura de Público e Lucro Estimado
É possível ir além? É sim. Embora não tenhamos dados para avaliar o que acontece na região < 500, podemos definir algumas premissas que possam fazer sentido. Por exemplo, vimos que o score é capaz de ordenar as pessoas de acordo com sua propensão a conversão.
Dessa forma, é plausível assumir que a conversão nas bandas em que não temos dados será proporcional a conversão nas bandas em que temos dados. Podemos assumir, por exemplo, que a conversão em cada banda é cada vez pior do que na banda anterior. É um chute educado e conversador.
result = df.groupby(["score_band", "campaign"])[['predicted_conversion']].mean().unstack()
count = df.groupby(["score_band", "campaign"])[['predicted_conversion']].count().unstack()
score_bands = ['900-999', '800-899', '700-799', '600-699', '500-599', '400-499', '300-399', '200-299', '100-199', '0-99']
increase = -0.07
for i in range(2, len(score_bands)):
result.loc[score_bands[i]] = result.loc[score_bands[i-1]] * (1 + increase)
increase -= 0.02
result = result.round(4)
display(result)
display(count)
| Score Band | A1 (%) | A2 (%) | B1 (%) | B2 (%) |
|---|---|---|---|---|
| 0-99 | 29.58 | 15.03 | 13.45 | 14.79 |
| 100-199 | 37.45 | 19.03 | 17.02 | 18.72 |
| 200-299 | 46.23 | 23.49 | 21.01 | 23.12 |
| 300-399 | 55.70 | 28.30 | 25.32 | 27.85 |
| 400-499 | 65.53 | 33.29 | 29.79 | 32.76 |
| 500-599 | 75.32 | 38.27 | 34.24 | 37.66 |
| 600-699 | 84.63 | 43.00 | 38.47 | 42.31 |
| 700-799 | 93.00 | 47.25 | 42.27 | 46.50 |
| 800-899 | 100.00 | 50.81 | 45.45 | 50.00 |
| 900-999 | 100.00 | 59.06 | 44.23 | 59.26 |
| Score Band | A1 | A2 | B1 | B2 |
|---|---|---|---|---|
| 0-99 | 5 | 4 | 42 | 39 |
| 100-199 | 6 | 1 | 51 | 46 |
| 200-299 | 7 | 7 | 41 | 48 |
| 300-399 | 5 | 9 | 45 | 50 |
| 400-499 | 5 | 3 | 41 | 47 |
| 500-599 | 50 | 50 | 403 | 472 |
| 600-699 | 59 | 50 | 467 | 450 |
| 700-799 | 44 | 53 | 457 | 439 |
| 800-899 | 481 | 433 | 55 | 54 |
| 900-999 | 424 | 469 | 52 | 54 |
Isso significa que podemos estimar o lucro de cada banda, ainda que não tenhamos dados suficientes. Observe como parece fazer sentido ter lucro nas regiões além do score 500.
revenue = result * 250
campaign_costs = {'A1': 150, 'A2': 120, 'B1': 50, 'B2': 80}
profit = revenue.copy()
for campaign, cost in campaign_costs.items():
profit[('predicted_conversion', campaign)] -= cost
profit
| Score Band | A1 (R$) | A2 (R$) | B1 (R$) | B2 (R$) |
|---|---|---|---|---|
| 0-99 | -76,05 | -82,43 | -16,38 | -43,03 |
| 100-199 | -56,38 | -72,43 | -7,45 | -33,20 |
| 200-299 | -34,43 | -61,28 | 2,53 | -22,20 |
| 300-399 | -10,75 | -49,25 | 13,30 | -10,38 |
| 400-499 | 13,83 | -36,78 | 24,48 | 1,90 |
| 500-599 | 38,30 | -24,33 | 35,60 | 14,15 |
| 600-699 | 61,58 | -12,50 | 46,18 | 25,78 |
| 700-799 | 82,50 | -1,88 | 55,68 | 36,25 |
| 800-899 | 100,00 | 7,03 | 63,63 | 45,00 |
| 900-999 | 100,00 | 27,65 | 60,58 | 68,15 |
Podemos estimar como teria sido cada banda se não existisse uma restrição de volume e existisse a mesma quantidade de usuários das outras bandas. Para isso, podemos calcular o lucro total projetado a partir desse lucro individual, também projetado.
count['total'] = count.sum(axis=1)
count['region'] = pd.cut(
count.index.map(lambda x: int(x.split('-')[0])),
bins=[-float('inf'), 499, 799, float('inf')],
labels=['< 500', '500-800', '> 800']
)
profit['region'] = pd.cut(
profit.index.map(lambda x: int(x.split('-')[0])),
bins=[-float('inf'), 499, 799, float('inf')],
labels=['< 500', '500-800', '> 800']
)
profit['count'] = count['total']
profit['total_profit'] = profit.apply(lambda row:
row[('predicted_conversion', 'A1')] * row['count'] if row.name in ['800-899', '900-999']
else row[('predicted_conversion', 'B1')] * row['count'], axis=1)
profit['estimated_count'] = 1000
profit['estimated_profit'] = profit['total_profit'] = profit.apply(lambda row:
row[('predicted_conversion', 'A1')] * row['estimated_count'] if row.name in ['800-899', '900-999']
else row[('predicted_conversion', 'B1')] * row['estimated_count'], axis=1)
profit| Score Band | A1 (R$) | A2 (R$) | B1 (R$) | B2 (R$) | Region | Count | Total Profit (R$) | Estimated Count | Estimated Profit (R$) |
|---|---|---|---|---|---|---|---|---|---|
| 0-99 | -76,05 | -82,43 | -16,38 | -43,03 | < 500 | 90 | -1.473,75 | 1000 | -16.375,00 |
| 100-199 | -56,38 | -72,43 | -7,45 | -33,20 | < 500 | 104 | -774,80 | 1000 | -7.450,00 |
| 200-299 | -34,43 | -61,28 | 2,53 | -22,20 | < 500 | 103 | 260,08 | 1000 | 2.525,00 |
| 300-399 | -10,75 | -49,25 | 13,30 | -10,38 | < 500 | 109 | 1.449,70 | 1000 | 13.300,00 |
| 400-499 | 13,83 | -36,78 | 24,48 | 1,90 | < 500 | 96 | 2.349,60 | 1000 | 24.475,00 |
| 500-599 | 38,30 | -24,33 | 35,60 | 14,15 | 500-800 | 975 | 34.710,00 | 1000 | 35.600,00 |
| 600-699 | 61,58 | -12,50 | 46,18 | 25,78 | 500-800 | 1026 | 47.375,55 | 1000 | 46.175,00 |
| 700-799 | 82,50 | -1,88 | 55,68 | 32,50 | 500-800 | 993 | 55.285,28 | 1000 | 55.675,00 |
| 800-899 | 100,00 | 7,03 | 63,63 | 45,00 | > 800 | 1023 | 102.300,00 | 1000 | 100.000,00 |
| 900-999 | 100,00 | 27,65 | 60,58 | 68,15 | > 800 | 999 | 99.900,00 | 1000 | 100.000,00 |
Se somente somarmos o Total Profit total, teremos R$ 353.925,00, que é um valor bastante próximo ao que obtivemos otimizando somente na região > 500. Entretanto, se atendêssemos todos usuários em que o lucro é positivo, ou seja, > 200, poderíamos usar o Estimated Profit. Isso nos levaria a R$ 375.501,45.
profit[~profit.index.isin(['100-199', '0-99'])]['estimated_profit'].sum() + profit[profit.index.isin(['100-199', '0-99'])]['total_profit'].sum()Conclusão: O Equilíbrio entre Dados e Premissas
Em termos financeiros, não é uma mudança tão significativa. Entretanto, atinge uma quantidade muito maior de usuários ao deixar de segmentar somente para > 500.
Ainda que esses números não tenham sido efetivamente observados nos dados, são premissas aceitáveis. Seria possível, por exemplo, aumentar o volume de forma gradual nas regiões não atendidas hoje para que eles fossem validados com risco controlado.
No fim das contas, essa análise mostra que decisões mais inteligentes vêm de uma combinação entre insights baseados nos dados existentes e premissas bem fundamentadas — mesmo que nem sempre estejam 100% validadas.
Se você gostou desse conteúdo, se inscreva na newsletter abaixo para receber todos os novos artigos e nos vemos no próximo! 😄



