Como os Transformers prestam atenção?

Transformers são a espinha dorsal da IA moderna. E no centro da arquitetura, está um mecanismo essencial: atenção escalada. Neste artigo, vamos explorar com profundidade esse componente — da teoria ao código, da álgebra linear ao aprendizado pronominal. Esta é a Parte 1 de uma série que vai dissecar os elementos fundamentais do Transformer. Aqui, o foco está na atenção. Nos próximos, vamos falar sobre embeddings, múltiplas cabeças, arquitetura do encoder, e muito mais.

🔍 Quer ver isso ganhando vida no código?

No meu canal do YouTube, eu mostro passo a passo como essa lógica se traduz em vetores reais, tensores PyTorch e visualizações interpretáveis.
🎥 Acesse: youtube.com/@francisquiniai

O passado: RNNs, LSTMs e seus limites

Antes de entender a revolução, precisamos lembrar do que veio antes. RNNs e LSTMs dominavam o processamento de sequências por anos. Tinham memória, passavam informações passo a passo e funcionavam bem para tarefas como modelagem de linguagem, tradução e reconhecimento de fala. Mas havia um limite prático difícil de superar: o custo do processamento sequencial. Cada palavra precisava esperar pela anterior para ser processada, o que dificultava paralelização e tornava o aprendizado de relações de longo prazo um desafio. Além disso, a memória das RNNs não era confiável para sequências longas — a informação se diluía.

A revolução: Attention is All You Need

Foi em 2017 que Vaswani e colegas publicaram o artigo Attention is All You Need. Nele, apresentaram o Transformer, uma arquitetura que eliminava completamente a recorrência. A proposta parecia ousada: em vez de processar as palavras em sequência, o modelo consideraria todas ao mesmo tempo. E faria isso aprendendo a "prestar atenção" nas partes mais relevantes do input. Com isso, destravou-se a paralelização total, aumentou-se a capacidade de capturar dependências de longo prazo e, de quebra, abriu-se caminho para arquiteturas maiores, com mais dados e mais contexto.

Mas o que é, de fato, essa atenção? Qual a matemática por trás dela?

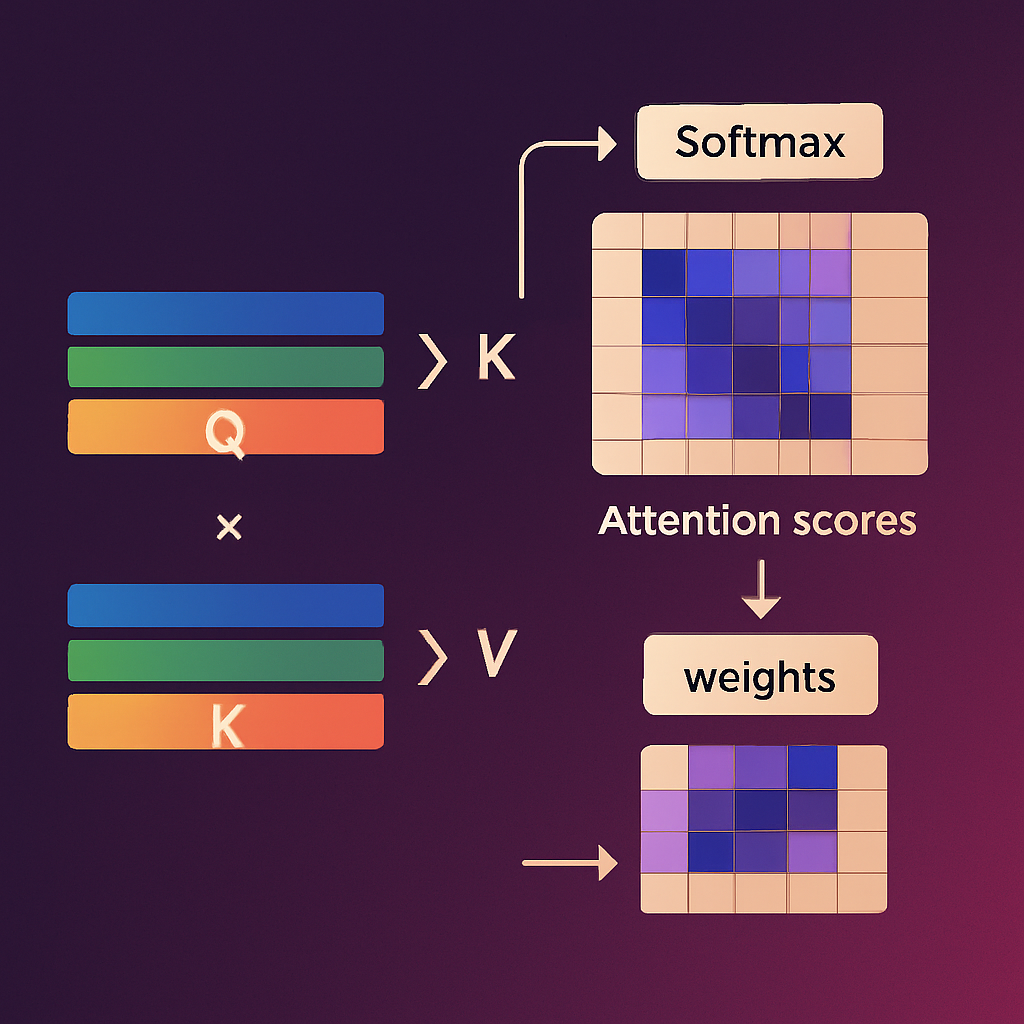
A atenção é uma operação baseada em produto escalar entre vetores. Para cada palavra da sequência, geramos três vetores: %%\textbf{query} ((Q))%%, %%\textbf{key} ((K))%% e %%\textbf{value} ((V))%%. A ideia é que a query represente o que a palavra está buscando, a key represente o que as demais palavras oferecem e o value contenha a informação associada a cada uma.

Calculamos a similaridade entre a query de uma palavra e todas as keys das palavras da sequência usando produto escalar, resultando em uma matriz de escores de atenção:

%% \text{scores} = \frac{QK^\top}{\sqrt{d_k}} %%

Em seguida, aplicamos uma função %%\textit{softmax}%% para normalizar os escores e obter os pesos de atenção:

%%\text{weights} = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)%%

Esses pesos são usados para calcular uma média ponderada dos valores (V), produzindo a saída da atenção:

%% \text{output} = \text{weights} \cdot V %%

Esse vetor resultante representa um novo estado da palavra, agora incorporando contexto de outras palavras relevantes da sequência.

Um exemplo interpretável

Imagine a frase:

Input: "A inteligência artificial está transformando o mundo"

O modelo vai gerar vetores Q, K e V para cada uma das palavras da frase. Por simplicidade, vamos assumir que temos vetores com 4 dimensões para cada token. A atenção para a palavra "transformando", por exemplo, será influenciada por tokens como "inteligência" e "mundo", se os vetores estiverem alinhados em suas direções semânticas. O produto escalar entre Q de "transformando" e os K das demais palavras vai definir o quanto cada uma pesa na combinação final.

Um exemplo mais real e interpretável:

Input: "Maria entregou o relatório para Ana porque ela estava no escritório."

Essa frase é ambígua: quem estava no escritório? Maria ou Ana?

Em modelos treinados como BERT, a matriz de atenção da palavra "ela" mostra forte peso em "Ana", indicando que o modelo aprendeu, com base em corpus e contexto, que é mais provável que a referência seja Ana. Isso acontece porque os vetores de Q, K e V foram ajustados durante o treinamento para capturar padrões estatísticos e relacionamentos linguísticos. Os pesos de atenção expressam essas relações.

Como os pesos são aprendidos?

A resposta está nas matrizes W_q, W_k e W_v. Elas são parâmetros treináveis que transformam os embeddings de entrada nos vetores Q, K e V. Durante o treinamento, o erro na tarefa (ex: predição da próxima palavra) é propagado de volta por meio da atenção, e essas matrizes são ajustadas com gradiente descendente.

Com o tempo, o modelo aprende que certas combinações de vetores ativam corretamente os relacionamentos mais úteis. Assim, ele passa a "olhar" para os tokens certos nas horas certas. Não porque alguém programou isso, mas porque aprender a fazer isso reduz o erro na tarefa final.

Código básico da atenção com NumPy

O código a seguir implementa a lógica da atenção de forma explícita usando NumPy. Começamos com uma sequência de três palavras representadas como vetores em um espaço de 4 dimensões. Multiplicamos esses vetores pelas matrizes aprendidas W_q, W_k, W_v​, que simulam os parâmetros do modelo, para obter os vetores de consulta (Q), chave (K) e valor (V). O produto escalar entre Q e a transposta de K mede a similaridade entre palavras. Em seguida, aplicamos uma normalização via softmax para gerar os pesos de atenção. Finalmente, realizamos uma combinação ponderada dos vetores V com esses pesos para obter a saída final: um novo vetor contextualizado para cada palavra, considerando a relevância das outras. Este processo espelha exatamente o que acontece dentro de uma camada de atenção em Transformers.

import numpy as np

# Sequência de 3 palavras, cada uma com 4 dimensões
x = np.random.rand(3, 4)

# Matrizes W aprendidas (para Q, K e V)
W_q = np.random.rand(4, 4)
W_k = np.random.rand(4, 4)
W_v = np.random.rand(4, 4)

Q = x @ W_q
K = x @ W_k
V = x @ W_v

# Produto escalar entre Q e K transposta
scores = Q @ K.T / np.sqrt(4)
weights = np.exp(scores) / np.exp(scores).sum(axis=1, keepdims=True)

# Output final
attention = weights @ V

Código modular com PyTorch

Antes de vermos como tudo isso é utilizado na prática, vale encapsular a lógica da atenção escalada em um módulo reutilizável. A implementação abaixo define exatamente a equação:

%%\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{Q K^T}{\sqrt{d_k}} \right) V%%

Essa operação é o núcleo da atenção em Transformers. Cada uma das várias cabeças de atenção do modelo executa esse mesmo cálculo, mas com parâmetros distintos, permitindo que o Transformer observe a sequência sob múltiplas perspectivas ao mesmo tempo.

import torch
import torch.nn.functional as F

class ScaledDotProductAttention(torch.nn.Module):
    def forward(self, Q, K, V):
        d_k = Q.size(-1)
        scores = Q @ K.transpose(-2, -1) / d_k**0.5
        weights = F.softmax(scores, dim=-1)
        return weights @ V

Esse módulo é o núcleo da atenção escalada. Ele é utilizado em cada uma das múltiplas cabeças de atenção no Transformer, permitindo que o modelo enxergue o input de diferentes perspectivas simultaneamente.

A atenção permite que o modelo entenda relações de longo alcance de forma eficiente. Em tradução, isso significa que o modelo consegue conectar um sujeito no início da frase com um verbo no final. Em geração de texto, que ele pode lembrar do estilo e do tom de uma introdução enquanto escreve a conclusão. E tudo isso sem loops, sem recursão, com pura álgebra linear — totalmente paralelizável em GPUs modernas.

Um experimento real: atenção aprendendo referência pronominal

Vamos observar o processo de aprendizado na prática. Vamos treinar uma rede pequena para que ela aprenda que a palavra "ela" em uma frase deve focar sua atenção em "Maria".

Agora vamos observar, passo a passo, como a atenção aprende a capturar uma referência pronominal. Esse é um experimento didático com poucos tokens, vetores pequenos e total transparência nas operações.

Objetivo

Queremos que a atenção da palavra "ela" aprenda a focar na palavra "Maria". Nossa frase de treino será:

"João deu Maria ela"

O vocabulário é composto por apenas 4 palavras:

João, deu, Maria, ela

Atribuímos os índices:

João = 0, deu = 1, Maria = 2, ela = 3

Embeddings iniciais

Cada palavra é representada por um vetor de embedding de dimensão 3 (inicializados aleatoriamente):

[[ 0.1013,  1.3199, -0.8060],  # João
 [-0.3447,  2.1137, -1.3133],  # deu
 [ 0.7930,  0.3330,  0.9407],  # Maria
 [-0.8380, -2.0299, -1.1218]]  # ela

Geração dos vetores Q, K e V

Cada embedding é projetado em três espaços diferentes por matrizes treináveis:

• Q (query): representa o que a palavra está buscando
• K (key): representa o que a palavra oferece
• V (value): representa a informação da palavra

As projeções seguem:

%% Q = X W_q \quad,\quad K = X W_k \quad,\quad V = X W_v %%

Com valores numéricos gerados na primeira época (exemplo real):

Q = 
[[-0.2001, 0.3570, 0.5615],
[-0.0999, 0.5520, 0.8895],
[-1.0008, 0.2845, -0.2464],
[ 1.8992, -0.9212, -0.0309]]

K =
[[ 0.0473, -0.6073,  0.1295],
 [ 0.0513, -1.2269,  0.4704],
 [-0.2684,  0.3256, -0.6502],
 [ 0.5608,  0.3946,  0.7527]]

V =
[[-0.7065,  0.7598, -0.2885],
 [-1.2361,  1.4640, -0.6187],
 [ 0.3903, -0.6640,  0.1630],
 [ 0.0844,  0.1751,  0.2359]]

Produto escalar entre Q e K

O coração da atenção é o produto escalar entre queries e keys, seguido de uma normalização:

%% \text{scores} = \frac{Q K^\top}{\sqrt{d_k}} %%

Com isso, temos os scores de atenção entre cada par de palavras:

Scores =
[[-0.0886, -0.1063, -0.1127,  0.2606],
 [-0.1297, -0.1524, -0.2146,  0.4799],
 [-0.1455, -0.2980,  0.3011, -0.3663],
 [ 0.3725,  0.7003, -0.4559,  0.3917]]

Aplicação do softmax

Transformamos os scores em probabilidades com softmax. Cada linha agora representa a distribuição de atenção de uma palavra sobre as demais:

Pesos (linha de "ela") =
[0.2601, 0.3611, 0.1136, 0.2652]

Nosso objetivo é que esse vetor evolua até:

Target: [0, 0, 1, 0]

Ou seja, a palavra "ela" deve olhar apenas para "Maria".

Função de perda

Utilizamos o erro quadrático médio (MSE):

%% \mathcal{L} = \frac{1}{n} \sum_{i=1}^n (a_i - t_i)^2 %%

Com valor inicial de:

Loss = 0.2635

Aprendizado ao longo do tempo

À medida que o modelo treina, ele ajusta suas matrizes de projeção. Isso faz com que os vetores Q, K e V mudem, e os pesos de atenção também.

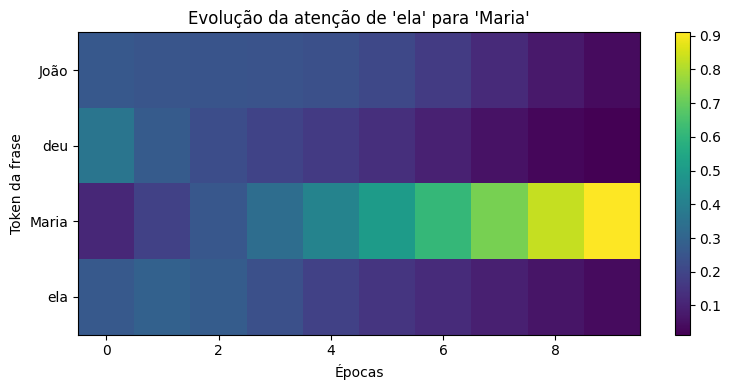
Veja como o vetor de atenção de "ela" evolui ao longo das épocas:

Época 0: [0.2601, 0.3611, 0.1136, 0.2652]
Época 3: [0.2411, 0.1934, 0.3335, 0.2320]
Época 5: [0.2080, 0.1335, 0.5052, 0.1533]
Época 7: [0.1216, 0.0585, 0.7267, 0.0932]
Época 9: [0.0389, 0.0134, 0.9097, 0.0380]

Convergência

Depois de poucas épocas, a atenção da palavra "ela" se concentra quase totalmente em "Maria", como queríamos.

Atenção final: [0.0389, 0.0134, 0.9097, 0.0380]
Perda final: 0.0028

Esse experimento mostra o processo completo: inicialização aleatória, cálculos da atenção, retropropagação do erro e ajuste dos pesos. Em poucas épocas, mesmo uma rede pequena aprende dependências sutis — como que "ela" se refere a "Maria".

O gráfico a seguir ilustra a evolução dos pesos de atenção conforme a evolução das épocas de treino.

No fundo, tudo é álgebra linear. Mas com as parametrizações certas, os Transformers aprendem coisas poderosas. Transformers são o núcleo das LLMs modernas, mas não são tudo. Eles representam a base matemática e arquitetural que tornou possível lidar com sequências longas de forma eficiente. No entanto, os modelos de linguagem atuais combinam essa base com escala massiva, pré-treinamento em grandes volumes de dados e técnicas de refinamento posteriores. Entender transformers é fundamental — mas é apenas uma parte da engenharia que sustenta a inteligência artificial contemporânea.