AttentionHead: como os Transformers ajustam seu foco para tarefas específicas?

No último post eu mostrei como funciona o mecanismo de atenção de um Transformer, mas aquela não é a história completa. Na verdade, o mecanismo de atenção tem mais algumas nuances para capturar informações que quero discutir nesse post. Antes de continuar, recomendo que você leia o post anterior para conseguir acompanhar (Transformers: como funciona o mecanismo de atenção).

O último código visto naquele post calculada o embedding após o mecanismo de atenção usando a query, keys e values.

query = v_key = value = inputs_embeds
dim_k = v_key.size(-1)
scores = torch.bmm(query, v_key.transpose(1, 2))/sqrt(dim_k)

weights = F.softmax(scores, dim=-1)

attn_outputs = torch.bmm(weights, value)

print(attn_outputs)

Para facilitar o decorrer desse artigo, vou encapsular esse processo em uma função que recebe query, key e value como parâmetro e realiza esses mesmos procedimentos, retornando o embedding final após a atenção e os pesos calculados.

def scaled_dot_product_attention(query, key, value):
    dim_k = query.size(-1)
    scores = torch.bmm(query, key.transpose(1, 2))/sqrt(dim_k)
    weights = F.softmax(scores, dim=-1)
    return torch.bmm(weights, value), weights

Query, Key e Values

Note que, nos exemplos até aqui, adotamos query, key e value iguais a inputs_embeds. Mas o que isso significa? Vamos explorar esses conceitos um pouco mais.

Imagine que você chega em uma festa com diversos grupos diferentes de pessoas conversando. Cada grupo está discutindo um tópico diferente: livros, filmes, tecnologia, etc. Você quer se juntar a um grupo, mas antes de decidir qual, você dá uma olhada geral para entender sobre o que cada grupo está falando. Essa "olhada geral" é um pouco como o mecanismo de atenção: ajuda a decidir em quais partes da informação (ou conversa) você deve se concentrar.

• query: É o assunto que você está interessado, vamos supor que seja "filmes". Ou seja, ao chegar a festa você está buscando por grupos que estejam falando sobre "filmes".
• key: É o tópico falado em cada grupo. Alguns podem ser mais relevantes para o seu interesse do que outros, pois não necessariamente existe um grupo falando especificamente sobre "filmes". Talvez exista um grupo falando sobre "atores" ou outro sobre "livros".
• value: São os detalhes da conversa de cada grupo. Se o tópico é relevante para você, os detalhes dessa conversa se tornam importantes. É com base nesses detalhes que você determinará se aquele assunto vai, de fato, te interessar.

No nosso exemplo, o que significa adotar query = key = value? Significa que você está usando a mesma base de informação (inputs_embeds) para formar sua percepção sobre todos os três aspectos da interação social na festa: o tópico de interesse (query), os tópicos sendo discutidos pelos grupos (key), e o conteúdo ou a substância das conversas (value). É como se você estivesse avaliando e interagindo com os grupos baseado em uma percepção direta e não modificada dos tópicos de conversa.

Neste cenário, você escuta um grupo "conversando sobre filmes" e isso significa "conversando sobre filmes". Você se junta ao grupo, escuta sobre "filmes", fala sobre "filmes" e leva consigo uma experiência sobre "filmes". Sua interação é direta e baseada na correspondência exata entre "filmes" e o que você escuta sobre os tópicos dos grupos.

O problema disso é que você pode passar ao lado de um grupo que está discutindo sobre "livros que viraram filmes" ou um outro grupo falando sobre "como a tecnologia tem sido usada nos filmes", ambos assuntos poderiam te interessar por possuir relação com seu interesse em "filmes". Entretanto, como sua busca é criteriosa e restrita em busca do tópico "filmes", você ignora esses grupos.

Talvez você já tenha entendido que, embora o mecanismo de atenção discutido até aqui seja poderoso, adotar query = key = value parece não explorar todo esse poder.

Transformações Lineares: a visão intuitiva

Os mecanismos de atenção, especialmente os Transformers, adotam transformações lineares para modificar os embeddings originais e gerar query, key e values diferentes. Isso acontece baseado na motivação de que diferentes representações dos dados de entrada podem ser criadas para servir a propósitos específicos: queries (Q), keys (K) e values (V).

Qual o propósito intuitivo dessa transformação em cada um desses valores? Em nosso exemplo da festa e dos grupos de conversa, a transformação é como um super fone de ouvido e de um óculos capazes de transformar a forma como você escuta e enxerga os assuntos dos grupos. Vou explicar melhor.

• transformação linear na query: quando uma transformação linear é aplicada à query em um mecanismo de atenção, a forma como o modelo prioriza e processa diferentes partes da informação disponível é modificada. Na analogia da festa, o super fone de ouvido ajusta sua "sensibilidade auditiva" para ser mais receptivo a conversas sobre filmes, tornando essas discussões mais "altas" ou mais proeminentes em sua percepção. Isso é como afinar seu interesse para se concentrar mais em filmes, fazendo com que você naturalmente preste mais atenção quando esse tópico surge.

O super fone de ouvido ajusta sua capacidade de ser mais receptivo as conversas sobre "filmes", mas ainda exigiria que você analisasse todos os grupos para ouvir e entender se faz sentido para você. Ou seja, você ainda precisaria ouvir os grupos e ver se estão falando sobre "filmes", você só estaria mais atento quando encontrasse um.

• transformação linear na key: com a transformação linear na key, o modelo ajusta sua percepção de relevância, tornando-o mais sensível a conexões indiretas ou temas relacionados que poderiam ser interessantes baseados nos interesses atuais (query). É como se, além dos super fones de ouvidos, você também tivesse óculos com a capacidade de "traduzir" visualmente a importância de cada conversa para seus interesses. Quando você olha para um grupo discutindo sobre algum tópico relacionado a "filmes", não apenas o volume das conversas é aumentado, mas os óculos destacam (talvez com um brilho ou um contorno luminoso) esses os grupos.

Dessa forma, você ganha um direcional de quais grupos você deve ouvir e prestar atenção primeiro para entender se estão falando sobre "filmes". Agora, além de ouvir esses grupos melhor, você tem uma ideia de quais são mais prováveis de estarem abordando o tópico "filmes" e direcionar sua atenção pra eles primeiro. Entretanto, você ainda precisa escutar o assunto da conversa para identificar se é, de fato, sobre "filmes".

• transformação linear no value: os values representam o conteúdo ou a substância das informações que serão agregadas e ponderadas com base na atenção calculada. Ao transformar os values, o modelo ajusta o impacto ou a importância dessas informações, enfatizando aspectos que são particularmente relevantes ou interessantes. É como se, além de aumentar o volume das conversas sobre filmes e destacar grupos com discussões relevantes, os óculos e fones também tivessem a capacidade de fazer com que certas palavras ou frases ditas nessas conversas ressoem mais para você. Quando alguém menciona algo diretamente relacionado aos seus interesses em "filmes" nesses grupos, essa parte da conversa não só soa mais alta, mas também fica mentalmente destacada para você, tornando-a mais memorável e influente na sua percepção da conversa.

Com todos esses mecanismos, você escuta os grupos que falam de assuntos relacionados a "filmes" com mais atenção e volume mais alto, você consegue focar em escutar eles primeiro pois estão visualmente mais destacados e, por fim, tem mais facilidade de identificar se estão, de fato, falando sobre "filmes" pois os tópicos da conversa relacionados a "filmes" são destacados em sua mente, tornando mais fácil descobrir se o assunto é de fato relevante.

Transformações Lineares: a visão matemática

Lembre-se que em nosso exemplo tínhamos o seguinte embedding:

• "o": torch.tensor([1.0, 1.0, 1.0]),
• "filme": torch.tensor([4.0, 2.0, 1.0]),
• "começa": torch.tensor([1.0, 4.0, 3.0]),
• "em": torch.tensor([1.0, 1.0, 1.0]),
• "breve": torch.tensor([1.0, 5.0, 4.0])

Cuja a matriz de embeddings é:

embedding_matrix = torch.stack(list(vocab_embeddings.values()))
print(embedding_matrix)

O processo de transformação linear envolve utilizar matrizes W_query, W_keye W_value para transformar query, key e value, respectivamente. Vamos adotar, por exemplo, a matriz W_query como sendo [[2, 0, 0], [0, 1, 0], [0, 0, 1]]. Quase uma identidade, mas aumentando a importância somente da primeira dimensão do embedding, que refere-se a "Entretenimento". Ou seja, você está mais atento a tópicos sobre entretenimento.

Se multiplicarmos essa matriz W_query pelo embedding original tensor([[1., 1., 1.], [4., 2., 1.], [1., 4., 3.], [1., 1., 1.], [1., 5., 4.]]), temos como resultado o embedding tensor([[2., 1., 1.], [8., 2., 1.], [2., 4., 3.], [2., 1., 1.], [2., 5., 4.]]). Note que a primeira coluna do tensor de entrada foi multiplicada por 2 (conforme a primeira coluna da matriz de transformação [2, 0, 0]), enquanto as outras duas colunas permaneceram inalteradas.

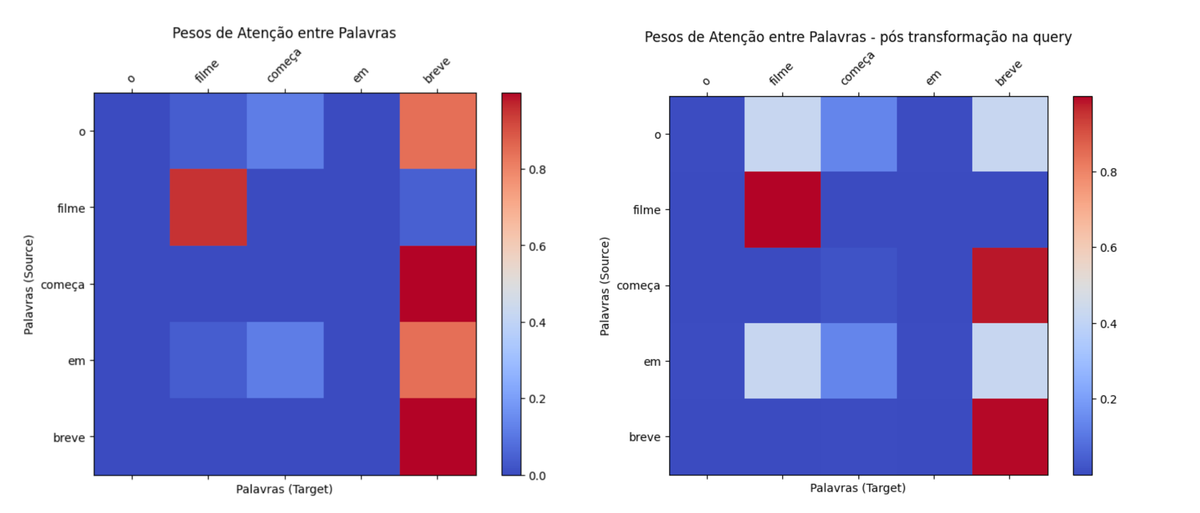
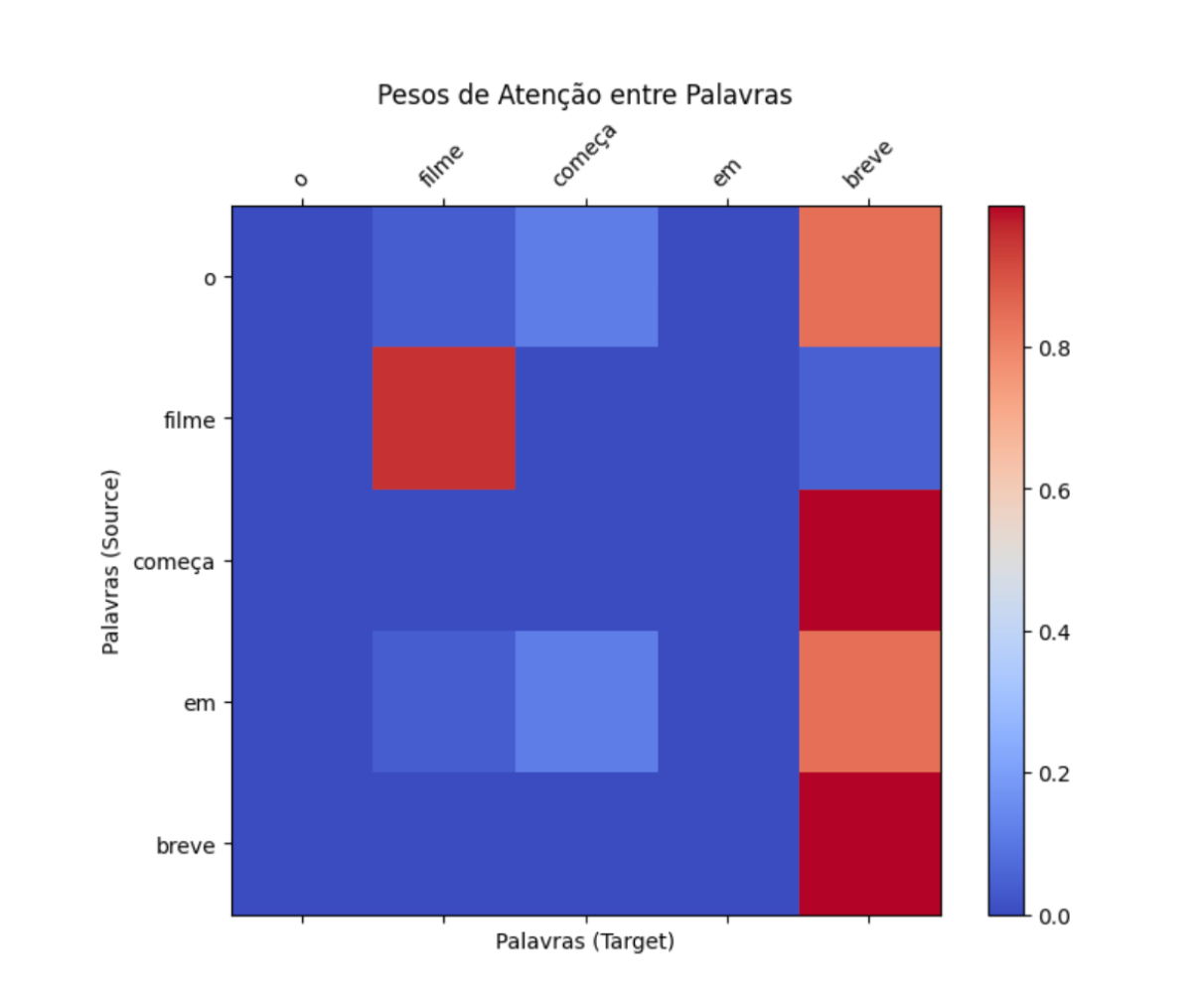
Vamos comparar os pesos de atenção do exemplo original com os pesos de atenção obtidos com essa transformação na query.

embedding_matrix_batch = embedding_matrix.unsqueeze(0)

query = key = value = embedding_matrix_batch

embedding_original, weights_original = scaled_dot_product_attention(query, key, value))

W_query = torch.tensor([[[2, 0, 0], 
                        [0, 1, 0], 
                        [0, 0, 1]]], dtype=torch.float)

query_transformada = torch.bmm(embedding_matrix_batch, W_query)

embedding_transformado, weights_transformado = scaled_dot_product_attention(query_transformada, key, value))

Analisando as diferenças entre weights_originale weights_transformado, repare como a atenção de "filme" para "filme" está ainda maior. Isso acontece pois aumentamos a relevância da primeira dimensão na query, ou seja, estamos mais atentos a tópicos relacionados a entretenimento. De forma similar, a atenção existente entre "em" e "breve" foi reduzida. Isso acontece pois, como estamos mais interessados em entretenimento, a atenção de tópicos relacionados a temporalidade é reduzida.

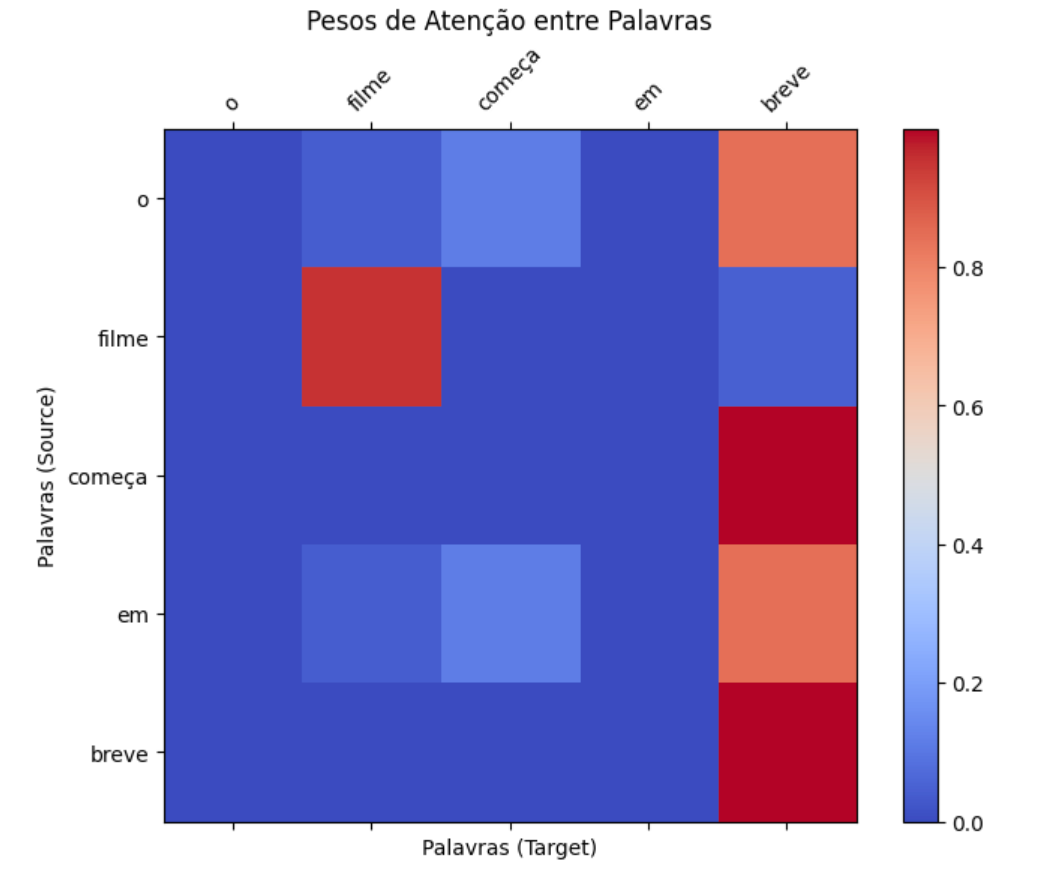
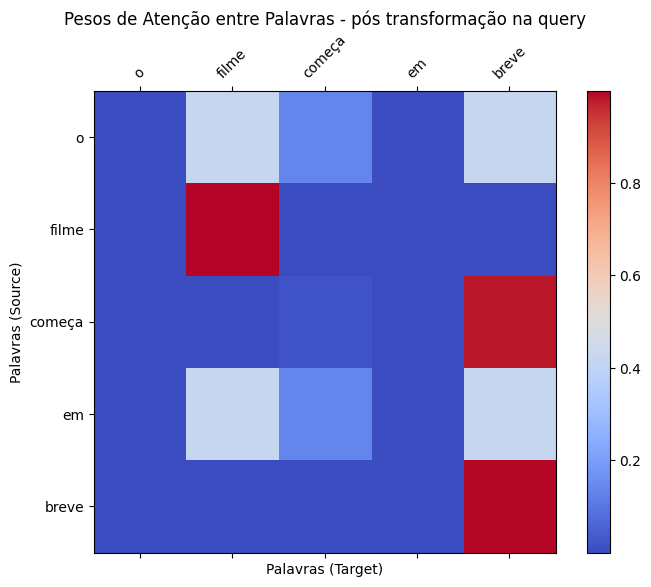
Vamos agora aplicar a transformação linear em query, key e valuee não apenas em query. Para isso, vou multiplicar keypor W_key = [[1, 0, 0], [0, 0.5, 0], [0, 0, 0.5]]. Ou seja, estamos multiplicando todas as dimensões, exceto a primeira, por 0.5. Isso significa que estamos reduzindo o peso das dimensões 2 e 3 na definição da key. Dessa forma vamos reduzir a relevância das outras dimensões e priorizar a primeira.

De forma similar, vamos multiplicar value por uma matriz identidade [[1, 0, 0], [0, 1, 0], [0, 0, 1]] como forma de apenas manter o value. Essa decisão é pelo fato de que a primeira dimensão do embedding é justamente a mais importante para a gente nesse momento.

embedding_matrix_batch = embedding_matrix.unsqueeze(0)

query = key = value = embedding_matrix_batch

W_query = torch.tensor([[[2, 0, 0], 
                        [0, 1, 0], 
                        [0, 0, 1]]], dtype=torch.float)

W_key = torch.tensor([[[1, 0, 0], 
                        [0, 0.5, 0], 
                        [0, 0, 0.5]]], dtype=torch.float)

W_value = torch.tensor([[[1, 0, 0], 
                        [0, 1, 0], 
                        [0, 0, 1]]], dtype=torch.float)

query = torch.bmm(embedding_matrix_batch, W_query)
key = torch.bmm(embedding_matrix_batch, W_key)
value = torch.bmm(embedding_matrix_batch, W_value)

attn_outputs, weights = scaled_dot_product_attention(query, key, value)

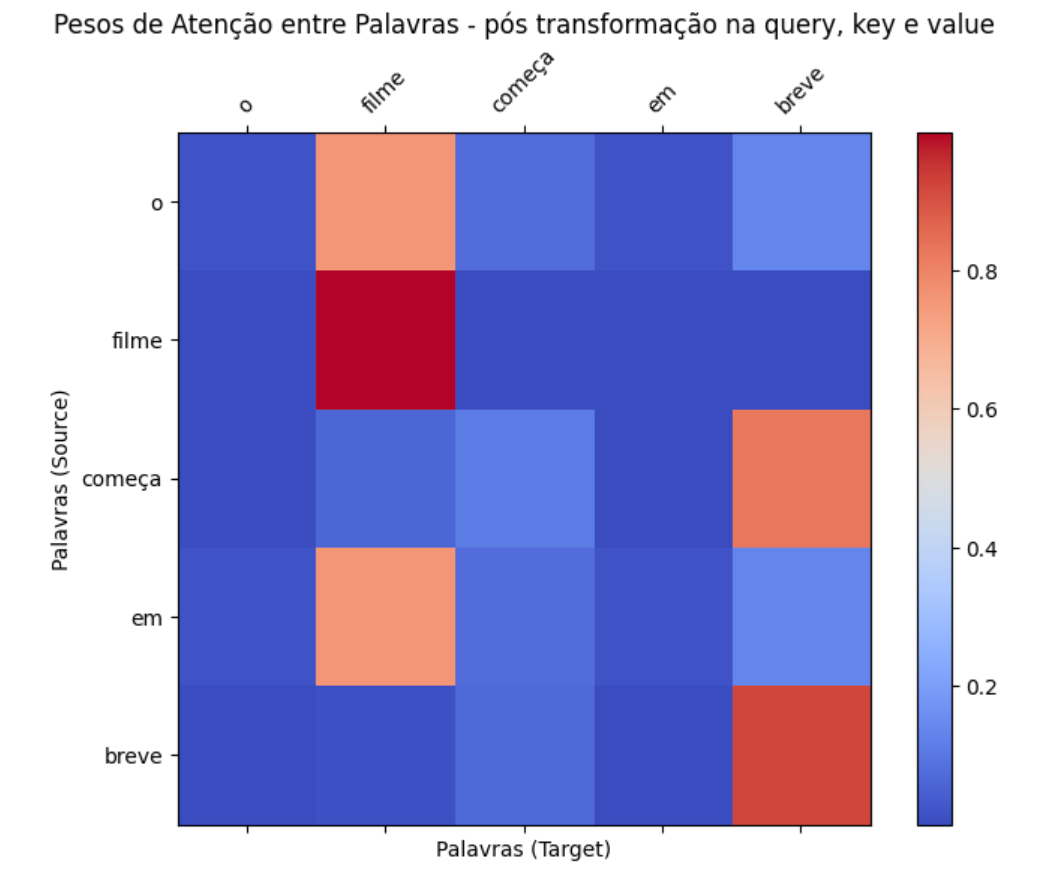
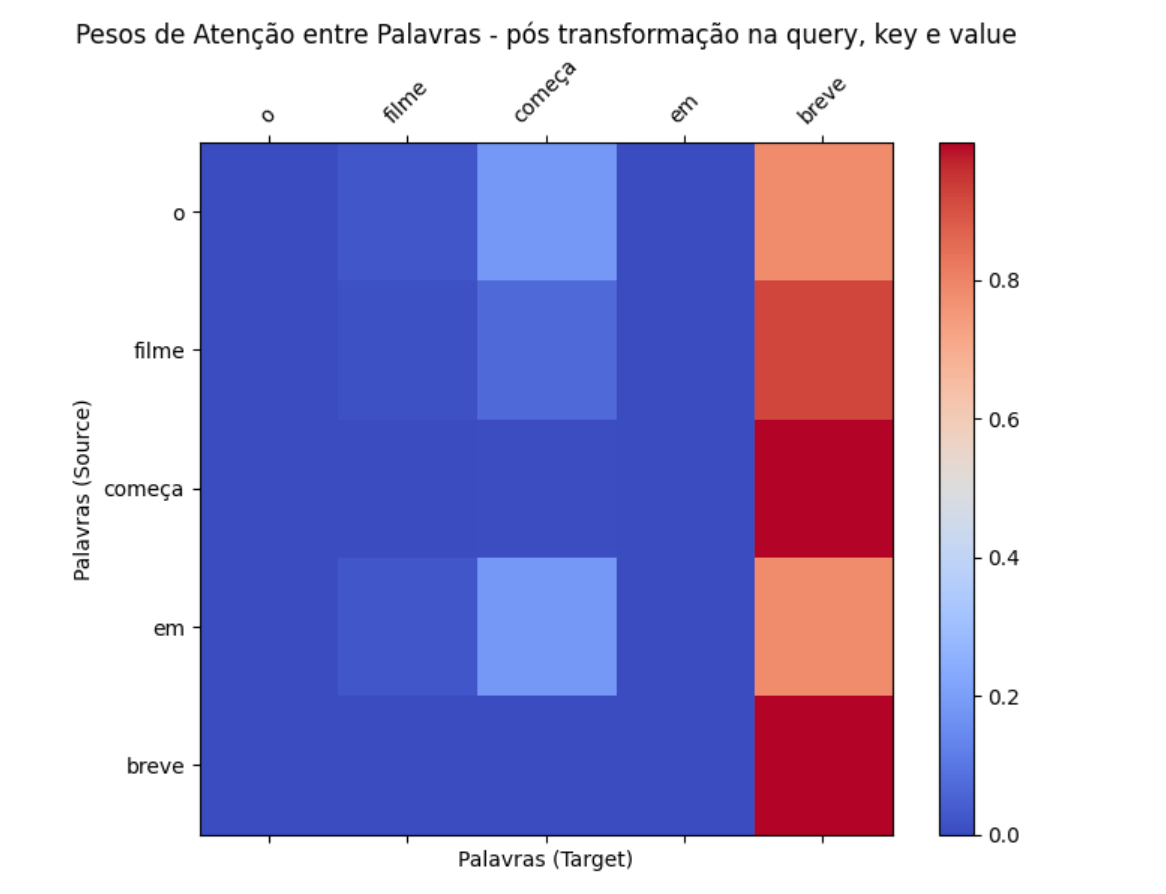
Repare como a matriz de atenção muda nos 3 cenários: sem nenhuma transformação, transformando somente a query e transformando a query, key e value. No último caso, a atenção está extremamente concentrada em torno de "filme", visto que fizemos nosso mecanismo direcionar sua atenção a "entretenimento".

O que aconteceria se, em vez de "entretenimento", estivéssemos interessados na dimensão "temporalidade"? Podemos observar esse efeito modificando as matrizes da transformação para refletir esse efeito.

• W_query: modificando para intensificar o efeito na segunda dimensão, temporalidade.
• W_key: modificando para reduzir a intensidade de todas as dimensões, exceto a segunda.
• W_value: modificando para inverter a ordem dos valores, trazendo a segunda dimensão para a primeira posição do embedding

Repare na matriz de atenção original e na matriz após essa transformação focada em temporalidade. Dessa vez, ao contrário da imagem anterior, a atenção foi deslocada para a dimensão temporalidade, destacando a atenção em torno dos itens que envolvem a palavra "breve" e reduzindo consideravelmente a atenção em torno de "filme", pois estamos mais interessados agora em temporalidade do que em entretenimento.

Attention Head com PyTorch

O cenário considerado até aqui é extremamente simples, adotando um embedding simplificado de 3 dimensões e matrizes de transformação manualmente definidas. Na prática, obviamente, isso não vai acontecer.

No nosso código somos capazes de calcular os pesos de atenção e o novo embedding com a função scaled_dot_product_attention, mas ainda estamos realizando a transformação linear de forma manual. Para resolver isso, vou criar uma classe chamada AttentionHead que será responsável não só por calcular a atenção, mas também por realizar a transformação linear.

class AttentionHead(nn.Module):
    def __init__(self, embed_dim, head_dim):
        super().__init__()
        self.q = nn.Linear(embed_dim, head_dim)
        self.k = nn.Linear(embed_dim, head_dim)
        self.v = nn.Linear(embed_dim, head_dim)

    def forward(self, hidden_state):
        attn_outputs, weights = scaled_dot_product_attention(self.q(hidden_state), self.k(hidden_state), self.v(hidden_state))
        return attn_outputs, weights

Note que estamos iniciando a classe com 3 matrizes de transformação linear: q (query), k (key) e v (value). Ao chamar scaled_dot_product_attention, estamos passando como parâmetro a transformação linear das queries, keys e values, não mais o valor original. Ou seja, estamos realizando a transformação linear de forma automática. A função forward é responsável por aplicar essas transformações, chamar a função que calcula a atenção e retornar o novo embedding pós atenção. Podemos simplesmente instanciar essa classe e usá-la para calcular o embedding após esse mecanismo de atenção com transformação linear.

custom_config = {
    'embed_dim': 3,
    'head_dim': 3
}
attention_head = AttentionHead(custom_config['embed_dim'], custom_config['head_dim'])
attn_output, weights = attention_head(embedding_matrix_batch)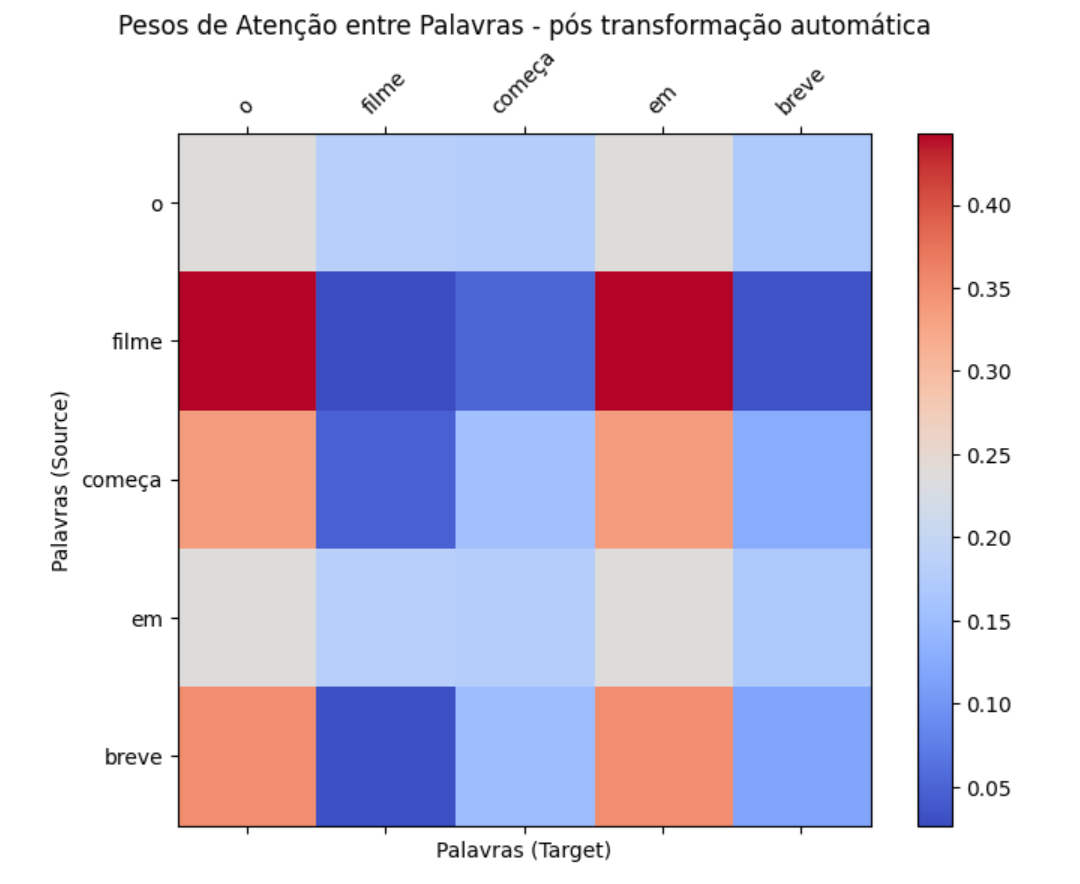

Note que o resultado de weights agora não faz tanto sentido mais. Parece mais como uma matriz aleatória em que não está claro por qual motivo e onde a atenção está concentrada. No contexto do mecanismo de atenção, as matrizes de transformação linear são inicialmente definidas com valores aleatórios ou seguindo alguma inicialização específica. Durante o processo de treinamento do modelo, essas matrizes são ajustadas automaticamente através do backpropagation, com base no gradiente da função de perda em relação aos pesos da rede.

Esse ajuste automático permite que o modelo melhore sua performance na tarefa específica para a qual está sendo treinado. Por exemplo, em uma tarefa de classificação de texto, o modelo aprenderá a ajustar as matrizes de transformação de forma que a atenção se concentre nas partes mais relevantes do texto para determinar a classe correta.

Ou seja, o modelo irá aprender como definir as matrizes de transformações lineares para melhorar sua habilidade de realizar aquela tarefa específica.

Quando definimos manualmente as matrizes de transformação, como nos exemplos anteriores, estamos essencialmente pré-configurando o modelo com uma noção inicial de quais aspectos dos dados devem ser enfatizados. Isso pode ser útil em cenários onde temos conhecimento prévio específico sobre a tarefa.

No entanto, o uso de transformações lineares automáticas e a capacidade do modelo de ajustar essas matrizes durante o treinamento oferecem uma flexibilidade maior. O modelo pode descobrir e adaptar-se às nuances dos dados de forma autônoma, sem a necessidade de intervenção manual para definir o foco da atenção.

Em resumo, a transição das matrizes de transformação manualmente ou aleatoriamente definida para as ajustadas automaticamente reflete a evolução de um modelo de atenção de uma configuração estática para uma adaptativa, onde o próprio modelo determina como melhor processar e dar peso às diferentes partes dos dados de entrada. Este aprendizado dinâmico é parte fundamental dos modelos de Transformer.

Conclusão

Espero que essa post tenha te ajudado a expandir seu conhecimento sobre o mecanismo de atenção, especialmente no que se refere a capacidade do modelo de aprender e adaptar o mecanismo de acordo com seu objetivo.

Pretendo continuar esse assunto explorando outros elementos de um modelo de PLN, além do Transformer. Se você tem interesse nesse assunto se inscreva para acompanhar os próximos artigos ou deixe um comentário sobre qual elemento te interessa mais 🙂